Thomas A. Anastasio
22 November 1999
Skip Lists were developed around 1989 by William Pugh1 of the University of Maryland. Professor Pugh sees Skip Lists as a viable alternative to balanced trees such as AVL trees or to self-adjusting trees such as splay trees.
The find, insert, and remove operations on ordinary
binary search trees are efficient, ![]() , when the input data is
random; but less efficient,
, when the input data is
random; but less efficient, ![]() , when the input data are ordered.
Skip List performance for these same operations and for any data set
is about as good as that of randomly-built binary search trees -
namely
, when the input data are ordered.
Skip List performance for these same operations and for any data set
is about as good as that of randomly-built binary search trees -
namely ![]()
In an ordinary sorted linked list, find, insert, and
remove are in ![]() because the list must be scanned
node-by-node from the head to find the relevant node. If somehow we
could scan down the list in bigger steps (``skip'' down, as it were),
we would reduce the cost of scanning. This is the fundamental idea
behind Skip Lists.
because the list must be scanned
node-by-node from the head to find the relevant node. If somehow we
could scan down the list in bigger steps (``skip'' down, as it were),
we would reduce the cost of scanning. This is the fundamental idea
behind Skip Lists.
In simple terms, Skip Lists are sorted linked lists with two differences:
We speak of a Skip List node having levels, one level per forward reference. The number of levels in a node is called the size of the node.
In an ordinary sorted list, insert, remove, and find
operations require sequential traversal of the list. This results in
![]() performance per operation. Skip Lists allow intermediate nodes
in the list to be ``skipped'' during a traversal - resulting in an
expected performance of
performance per operation. Skip Lists allow intermediate nodes
in the list to be ``skipped'' during a traversal - resulting in an
expected performance of ![]() per operation.
per operation.
To introduce the Skip List data structure, let's look at three list
data structures that allow skipping, but are not truly Skip Lists.
The first of these, shown in Figure 1 allows every
other node to be skipped in a traversal. The second, shown in
Figure 2 additionally allows every fourth node to be
skipped. The third, shown in Figure 3 additionally
allows every eighth node to be skipped, but suggests further
development of the idea to skipping every ![]() -th node.
-th node.
For all three pseudo-skip-lists, there is a header node and the nodes do not all have the same number of forward references. Every node has a reference to the next node, but some have additional references to nodes further along the list.
Here is pseudo-code for the find operation on each list. This same algorithm will be used with real Skip Lists later.
Comparable & find(const Comparable & X)
{
node = header node
for (reference level of node from (nodesize - 1) down to 0)
while (the node referred to is less than X)
node = node referred to
if (node referred to has value X)
return value of node referred to
else
return item_not_found
}
We start at the highest level of the header node and follow the references along this level until the value at the node referred to is equal to or larger than X. At this point, we switch to the next lower level and continue the search. Eventually, we shall be dealing with a reference at the lowest level of a node. If the next node has the value X, then we return that value; otherwise we return a value that signals unsuccessful search.
Figure 1 shows a 16-node list in which every second node has a reference two nodes ahead. The value stored at each node is shown below it (and corresponds in this example to the position of the node in the list). The header node has two levels; it's no smaller than largest node in the list. Node 2 has a reference to node 4, two nodes ahead. Similarly for nodes 4, 6, 8, etc - every second node has a reference two nodes ahead.
It's clear that the find operation does not need to visit
each node. It can skip over every other node, then do a final visit
at the end. The number of nodes visited is therefore no more than
![]() . For example, the nodes visited in
scanning for the node with value 15 would be
2, 4, 6, 8, 10, 12, 14, 16, 15,
a total of
. For example, the nodes visited in
scanning for the node with value 15 would be
2, 4, 6, 8, 10, 12, 14, 16, 15,
a total of
![]() .
.
Follow the algorithm for find on
page ![[*]](cross_ref_motif.gif) for this simple example to be sure
you understand it thoroughly.
for this simple example to be sure
you understand it thoroughly.
The second example is a list in which every second node has a reference two nodes ahead and additionally every fourth node has a reference four nodes ahead. Such a list is shown in Figure 2. The header is still no smaller than the largest node in the list.
The find operation can now make bigger skips than those for
the list in Figure 1. Every fourth node is skipped
until the search is confined between two nodes of size 3. At this
point, as many as three nodes may need to be scanned. It is also
possible that some nodes will be visited more than once using the
algorithm on page ![[*]](cross_ref_motif.gif) . The
number of nodes visited2 is no more than
. The
number of nodes visited2 is no more than
![]() . As an
example, look at the nodes visited in scanning for the node with value
of 15. These are 4, 8, 12, 16, 14, 16, 15 for a total of
. As an
example, look at the nodes visited in scanning for the node with value
of 15. These are 4, 8, 12, 16, 14, 16, 15 for a total of
![]() .
.
This final example is for a list in which some skip lengths are even larger.
Every ![]() -th node,
-th node,
![]() , has
a forward reference
, has
a forward reference ![]() nodes ahead. For example, every
nodes ahead. For example, every
![]() node has a reference 2 nodes ahead; every
node has a reference 2 nodes ahead; every ![]() node has a reference 8 nodes ahead, etc.
Figure 3 shows a short list of this type. Once again,
the header is no smaller than the largest node on the list. It is
shown arbitrarily large in the Figure.
node has a reference 8 nodes ahead, etc.
Figure 3 shows a short list of this type. Once again,
the header is no smaller than the largest node on the list. It is
shown arbitrarily large in the Figure.
Suppose the Skip List in Figure 3 contained 32 nodes
and consider a search in it. Working down from the
highest level, we first encounter node 16 and have cut the search in
half. We then search again, one level down in either the left or
right half of the list, again cutting the remaining search in half.
We continue in this manner till we find the sought-after node (or
not). This is quite reminiscent of binary search in an array and is
perhaps the best way to intuitively understand why the maximum number
of nodes visited in this list is in ![]() .
.
This data structure is looking pretty good, but there's a serious
problem with it for the insert and remove operations. The
work required to reorganize the list after an insertion or deletion is
in ![]() . For example, suppose that the first element is removed in
Figure 3. Since it is necessary to maintain the strict
pattern of node sizes, values from 2 to the end must be moved
toward the head and the end node must be removed. A similar situation
occurs when a new element is added to the list.
. For example, suppose that the first element is removed in
Figure 3. Since it is necessary to maintain the strict
pattern of node sizes, values from 2 to the end must be moved
toward the head and the end node must be removed. A similar situation
occurs when a new element is added to the list.
This is where the probabilistic approach of a true Skip List comes
into play. A Skip List is built with the same distribution of
node sizes, but without the requirement for the rigid pattern of node
sizes shown. It is no longer necessary to maintain the rigid pattern by
moving values around after a remove or insert operation. Pugh
shows that with high probability such a list still exhibits
![]() behavior. The probability that a given Skip List will
perform badly is very small.
behavior. The probability that a given Skip List will
perform badly is very small.
Figure 4 shows the list of Figure 3 with the nodes reorganized. The distribution of node sizes is exactly the same as that of Figure 3; the nodes just occur in a different pattern. In this example, the pattern would require that 50% of the nodes have just one reference, 25% have just two references, 12.5% have just three references, etc. The distribution of node sizes is maintained, but the strict order is not required.
Figure 4 shows one way this might work out. Of course, this is probabilistic, so there are many other possible node sequences that would satisfy the required probability distribution.
When inserting new nodes, we choose the size of the new node
probabilistically. Every Skip List has an associated (and fixed)
probability ![]() that determines the distribution of nodes. A fraction
that determines the distribution of nodes. A fraction
![]() of the nodes that have at least
of the nodes that have at least ![]() references also have
references also have ![]() references. The Skip List does not have to be reorganized when a new
element is inserted.
references. The Skip List does not have to be reorganized when a new
element is inserted.
Suppose we have an infinitely-long Skip List with associated
probability ![]() . This means that a fraction,
. This means that a fraction, ![]() , of the nodes with a
forward reference at level
, of the nodes with a
forward reference at level ![]() also have a forward reference at
level
also have a forward reference at
level ![]() .
.
Let ![]() be the fraction of nodes having precisely
be the fraction of nodes having precisely ![]() forward
references ( i.e.,
forward
references ( i.e., ![]() is the fraction of nodes of size
is the fraction of nodes of size ![]() ).
Then,
).
Then,
![]() and
and
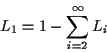
Since
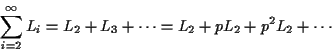
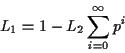
Recall that
![]() is the sum of the geometric
progression with first term
is the sum of the geometric
progression with first term ![]() and common ratio
and common ratio ![]() . Thus,
. Thus,
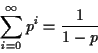
Therefore,
![]() . Since
. Since ![]() , we can
write
, we can
write
Example: In the situation shown in Figure 4,
![]() . Therefore,
. Therefore,
![]() of the nodes
with at least one reference have two references; one-half of those
with at least two references have three references, etc.
of the nodes
with at least one reference have two references; one-half of those
with at least two references have three references, etc.
You should work out the distribution for a SkipList with
associated probability of ![]() to be sure you
understand how distributions are computed.
to be sure you
understand how distributions are computed.
int generateNodeLevel(double p, int maxLevel)
{
int level = 1;
while (drand48() < p)
level++;
return (level > maxLevel) ? maxLevel : level;
}
Note that the level of the new node is independent of the number of nodes already in the Skip List. Each node is chosen only on the basis of the Skip List's associated probability.
When the associated probability is ![]() , the average number of comparisons
that must be done for find, is
, the average number of comparisons
that must be done for find, is
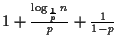 .
For example, for a list of size 65,536, the average number of nodes to be
examined is 34.3 for
.
For example, for a list of size 65,536, the average number of nodes to be
examined is 34.3 for
![]() and 35 for
and 35 for
![]() .
This is a tremendous improvement over an ordinary sorted list for which
the average number of comparisons is
.
This is a tremendous improvement over an ordinary sorted list for which
the average number of comparisons is
![]() .
.
The level of the header node is the maximum allowed level in the
SkipList and is chosen at construction.
Pugh shows that the maximum level should be chosen as
![]() . Thus, for
. Thus, for
![]() , the maximum
level for a SkipList of up to 65,536 elements should be chosen
no smaller than
, the maximum
level for a SkipList of up to 65,536 elements should be chosen
no smaller than
![]() .
.
The probability that an operation will take longer than expected is a
function of the probability associated with the list. For example,
Pugh calculates that for a list with ![]() and 4096 elements, the
probability that the actual time will exceed the expected time by a
factor of 3 is less than one in 200 million.
and 4096 elements, the
probability that the actual time will exceed the expected time by a
factor of 3 is less than one in 200 million.
The relative time and space performance of a Skip List depends on the probability level associated with the list. Pugh suggests that a probability of 0.25 be used in most cases. If the variability of performance is important, he suggests using a probability of 0.5 (variability decreases with increasing probability). Interestingly, the average number of references per node is only 1.33 when a probability of 0.25 is used. A binary search tree, of course, has 2 references per node, so Skip Lists can be more space-efficient.
SkipList implementation continued
public: SkipList(); // use max_node_size of 16, prob of 0.25 SkipList(int max_node_size, double probab); SkipList(const SkipList &); ~SkipList(); int getHighNodeSize() const; // size of the node with most levels int getMaxNodeSize() const; // max node size allowed in this list double getProbability() const; // prob for this list // insert item into this skiplist. void insert(const Comparable & item); // Search for item in skiplist. If found, return the item with // success equal true. Otherwise, return a dummy item with // success equal false. const Comparable & find(const Comparable & item, bool & success); // remove the first occurrence of the specified item void remove(const Comparable & item); private: // Search for item in this skiplist, starting at startnode // startnode will usually be the header. If item is found, // return the node at which it is found with success equal true. // Otherwise, return the preceding node with success equal false. // Precondition: startnode is not NULL SkipListNode * find(const Comparable & item, SkipListNode * startnode); // Accessor for _head SkipListNode * getHeader() const; // return the header nodecontinued below |
SkipList implementation continued
// Finds the point at which item would be inserted using a node // of the given size. // Returns a "lookback" node that has each of its forward // pointers set to the closest node (toward the header) at that level. SkipListNode * findInsertPoint(const Comparable & item, int nodesize); // insert item into this skiplist, using a node of the // specified size. success returned true if insertion succeeds void insert(const Comparable & item, int nodesize, bool & success); int _high_node_size; // highest-level node now in this list int _max_node_size; // highest-level node allowed in this list double _prob; // probability associated with this list SkipListNode * _head; // header node of this list }; // SkipList |
We will examine SkipList methods insert, and
remove in some detail below. Pseudocode
for find was given on page ![[*]](cross_ref_motif.gif) .
.
Insertion and deletion involve searching the SkipList to find the insertion or deletion point, then manipulating the references to make the relevant change.
When inserting a new element, we first generate a node that has had its level selected randomly. The SkipList has a maximum allowed level set at construction time. The number of levels in the header node is the maximum allowed. For convenience in searching, the SkipList keeps track of the maximum level actually in the list. There is no need to search levels above this actual maximum.
In Skip Lists, we need pointers to all the see-able previous nodes between the insertion point and the header. Imagine standing at the insertion point, looking back toward the header. All the nodes you can see are the see-able nodes. Some nodes may not be see-able because they are blocked by higher nodes. Figure 5 shows an example.
In the figure, the insertion point is between nodes 6 and 7. Looking
back toward the header, the nodes you can see at the various levels
are
level node seen
0 6
1 6
2 4
3 header
|
We construct a backLook node that has its forward pointers set to the relevant see-able nodes. This is the type of node returned by the findInsertPoint method.
The public insert(const Comparable &) method decides on the new
node's size by random choice, then calls the overloading private method
insert(const Comparable &,int,bool &) to do all the work.
template<class T>
void
SkipList<T>::insert(const T & item)
{
int nodesize = randomNodeSize(getProbability(), getMaxNodeSize());
insert(item, nodesize);
}
|
|
This is the private insert method.
template<class T>
void
SkipList<T>::insert(const T & item, int nodesize)
{
SkipList<T>::SkipListNode * backLook = findInsertPoint(item, nodesize);
SkipList<T>::SkipListNode * newnode =
new SkipList<T>::SkipListNode(item, nodesize);
// newnode may have more levels than are currently in list
// If so, adjust high_node_size of list.
if (nodesize > getHighNodeSize())
setHighNodeSize(nodesize);
// Rearrange the relevant previous pointers using information
// in the backLook node.
for (int i = 0; i < nodesize; i++)
{
SkipList<T>::SkipListNode * prev = backLook->getForward(i);
SkipList<T>::SkipListNode * next = prev->getForward(i);
newnode->setForward(i, next);
prev->setForward(i, newnode);
}
incrementListSize();
}
|
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation skip_lists.tex
The translation was initiated by Thomas Anastasio on 2000-02-19