











Tracing Functions
Sue Evans & James MacGlashan
Adapted from the CS1 Course at Swarthmore College by Lisa Meeden
Hit the space bar for next slide












Sue Evans & James MacGlashan
Adapted from the CS1 Course at Swarthmore College by Lisa Meeden
Hit the space bar for next slide
Let's trace the flow of code for this smaller example of our program and watch how the functions call each other.
def main():
verse("cow", "moo")
verse("pig", "oink")
main()
When we run the program flow follows the steps shown below with each item in red being the executed step. Make note that in the case of parameters, the parameter variable is assigned the value it's passed
When we run our program by entering python farm.py at the linux prompt, the system first encounters the definitions of the functions. It doesn't execute any of the functions until main() is called at the bottom of the file. For all programs, main() is always where execution begins.

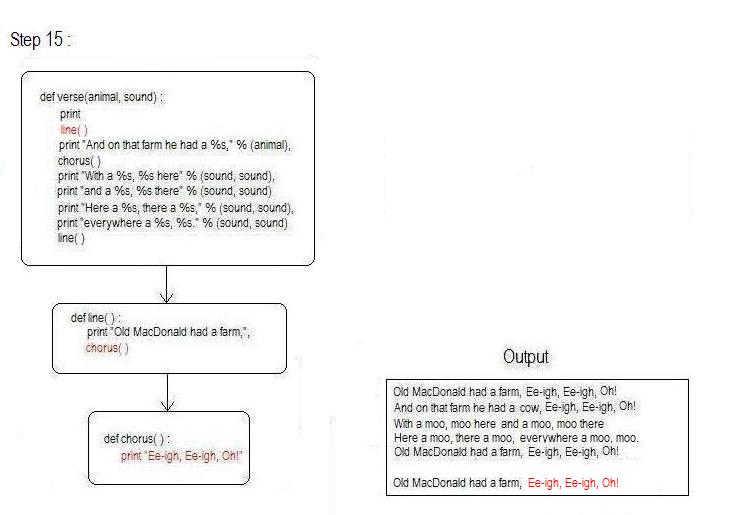
Once main() is called, the block of main()'s definition begins to execute. The first line of the block makes a call to the function verse(), passing "cow" and "moo". "cow" is assigned into the function's variable animal and "moo" into the function's variable sound. Then the first line of verse()'s body is executed, print, and a blank line is printed.
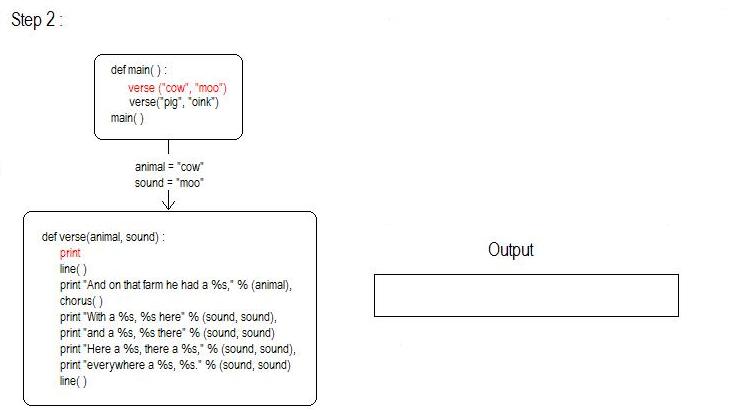
The function verse continues to execute. The next line of code makes a call to the function line() and the first statement of line() prints "Old MacDonald had a farm,". The comma at the end of the print statement keeps a newline from being printed so that future output can continue on the same line.
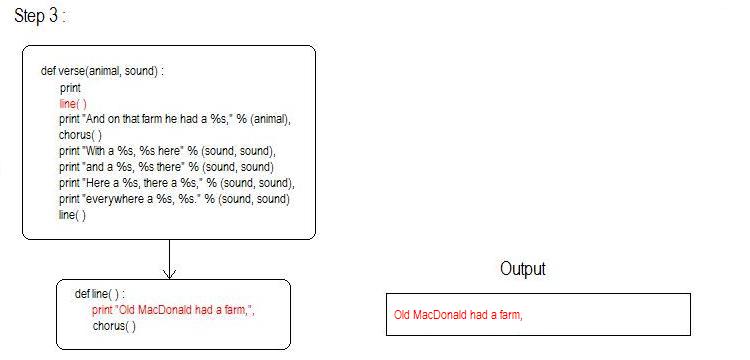
The function line() continues to execute and the function chorus() is called. The function chorus() contains only one line. It executes and "Ee-igh,Ee-igh, Oh!" is printed.

The function chorus is finished, so program control goes back to the function that called it, line(). The function line() is also finished, so control goes back to the function that called it, verse(). The next line in verse() is executed, printing "And on that farm he had a cow,", substituting the value of animal, currently "cow", into the string being printed to replace the %s.

The next line of verse() calls chorus. It prints "Ee-igh,Ee-igh, Oh!" and control returns back to the function that called it, verse().

verse() continues to execute, the next line printing "With a moo, moo here", where the value of sound, currently "moo", is substituted for each %s in the string.

Control continues on to the next line of verse, which prints "and a moo, moo there", again substituting the value of sound, "moo", into each %s in the string.

verse() continues to execute, its next line printing, "Here a moo there a moo,"

The next line prints, "everywhere a moo, moo".

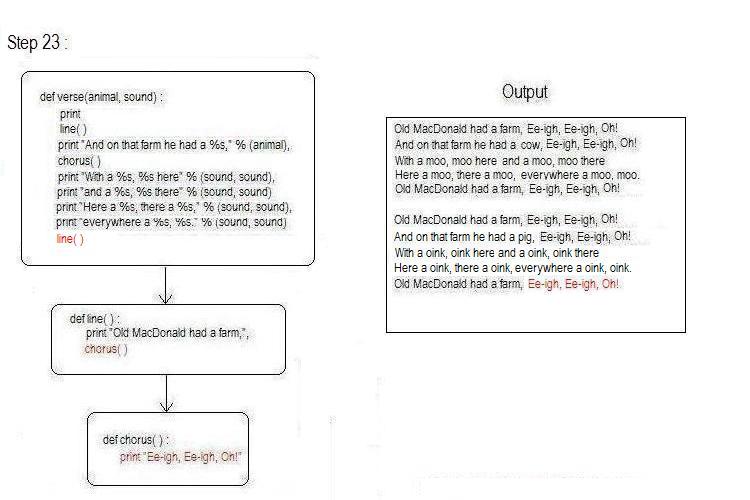
The next line of verse() makes a call to the function, line. The first line of line() prints "Old MacDonald had a farm,"

Control continues to the next line of line(), which makes a call
to the function, chorus. chorus prints "Ee-igh,Ee-igh,
Oh!" and control returns back to the calling function, line.
line is also finished, so control returns to verse().
verse is also finished, so control returns to main().
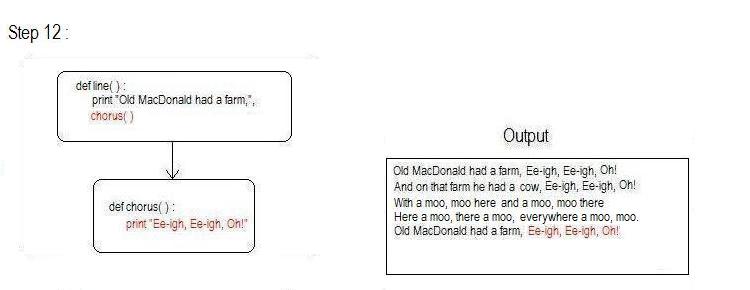
The next line of main() is a call to the function verse(), this time passing "pig" and "oink", where the variable animal will be assigned the value "pig" and sound will be assigned the value "oink".
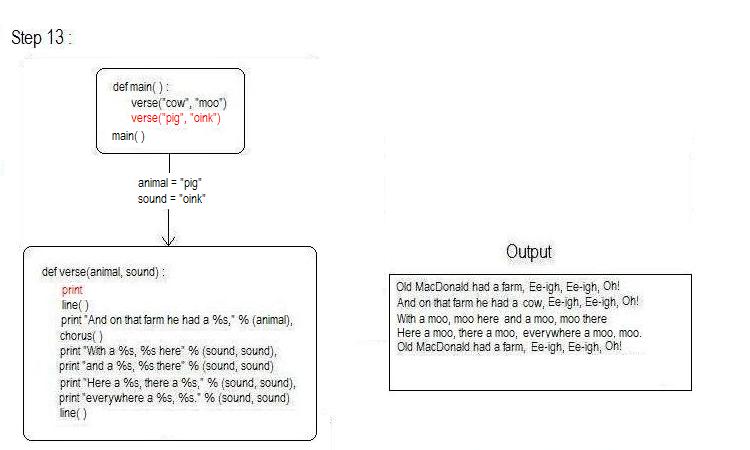
The flow of control will continue as it did for the first verse. Let's look at the second verse being formed, while keeping in mind that functions are not complete until their last line has finished. If that last line is a call to another function, the last line isn't complete until the control flow is returned from the called function.








>>> def addInterest(balance, rate): ... newBalance = balance * (1 + rate) ... balance = newBalance ... >>> amount = 1000 >>> rate = 0.05 >>> addInterest(amount, rate) >>> print amount
>>> print amount 1000
>>> def addInterest(balance, rate): ... newBalance = balance * (1 + rate) ... balance = newBalance ... >>> amount = 1000 >>> rate = 0.05 >>> addInterest(amount, rate) >>> print amount
>>> print amount 1000
>>> def noReturn(): ... print "This will not return a value" ... >>> x = noReturn() This will not return a value >>> print x None
>>> def stringReturn(): ... return "something" ... >>> x = stringReturn() >>> print x something >>> def floatReturn(): ... return 2.0 ... >>> x = floatReturn() >>> print x 2.0
>>> def addInterest(balance, rate): ... newBalance = balance * (1 + rate) ... return newBalance ... >>> amount = 1000 >>> rate = 0.05 >>> amount = addInterest(amount, rate) >>> print amount 1050
>>> def earlyReturn(): ... print "Entered the function" ... return 1.0 ... print "This line will not be reached" ... >>> x = earlyReturn() Entered the function >>> print x 1.0
>>> def absoluteValue(x): ... if x >= 0: ... return x ... return -1 * x ... >>> x = absoluteValue(5) >>> print x 5 >>> x = absoluteValue(-5) >>> print x 5
>>> def distance(x1, y1, x2, y2): ... xdiff = x1 - x2 ... ydiff = y1 - y2 ... return math.sqrt((xdiff * xdiff) + (ydiff * ydiff)) ... >>> dist = distance(0.0, 0.0, 1.0, 1.0) >>> dist 1.4142135623730951
>>> def square(x): ... return x * x ... >>> square(2) 4 >>> square(square(2)) 16
>>> def simplify(inches): ... feet = inches / 12 ... inches = inches % 12 ... return feet, inches ... >>> ft, inch = simplify(16) >>> ft 1 >>> inch 4 >>>
>>> length = simplify(16) >>> length (1, 4) >>>
>>> def getDimensions():
... length = input("Enter the length : ")
... width = input("Enter the width : ")
... height = input("Enter the height : ")
... return length, width, height
...
>>> lent, wid, ht = getDimensions()
Enter the length : 5
Enter the width : 6
Enter the height : 7
>>> lent
5
>>> wid
6
>>> ht
7
>>> dimens = getDimensions()
Enter the length : 5
Enter the width : 6
Enter the height : 7
>>> dimens
(5, 6, 7)
>>> lent, wid = getDimensions()
Enter the length : 5
Enter the width : 6
Enter the height : 7
Traceback (most recent call last):
File "<stdin>", line 1, in ?
ValueError: too many values to unpack
>>>
>>> gX = 5 >>> def scope1(): ... print gX ... >>> scope1() 5
>>> def scope2(): ... local1 = 7 ... print local1 ... >>> scope2() 7 >>> print local1 Traceback (most recent call last): File "<stdin>", line 1, in <module> NameError: name 'local1' is not defined
>>> gX = 5 >>> print gX 5 >>> def scope3(): ... gX = 10 ... print gX ... >>> scope3() 10 >>> print gX 5
>>> gX = 5 >>> print gX 5 >>> def scope4(): ... global gX ... gX = 10 ... print gX ... >>> scope4() 10 >>> gX 10
How many ways can you pick k items out of a set of n items?
The Program
# File: combine.py
# Author: Sue Evans
# Date: 9/29/09
# Section: All
# EMail: bogar@cs.umbc.edu
#
# This program tests a function to compute the
# mathematical combination function
# combinations(n, k), which gives the number
# of ways to choose a subset of k objects from
# a set of n distinct objects. It also uses
# one of our first modular functions, factorial().
# We'll be able to reuse it often.
# factorial() finds the factorial of the integer passed in
# Usage: f = factorial(n)
#
# Input: integer n for which to calculate n!
# Ouput: n! = n * n - 1 * n - 2 * ... * 3 * 2 * 1
def factorial(n):
product = 1
# finds product of all integers from 1 up to
# and including n, where product will finally
# hold the value of n!
for i in range (1, n + 1):
product *= i
return product
# combinations() calculates the number of ways to choose k
# items from a set of n items.
# Usage: ways = combinations(n, k)
#
# Inputs: n -- the number of distinct objects
# in the set
# k -- the number of objects to choose
# from the set
# Ouput: Number of ways to choose k from n
# see description below
#
# Assumptions:
# 1 <= n
# 1 <= k <= n
#
# Implements the combinations function, which
# returns the number of distinct ways of choosing
# k objects from a set of n objects. In
# mathematics, this function is often written as
# C(n,k), but a function called C is not very
# self-descriptive. Implements the formula
# n!/(k! * (n - k)!)
def combinations(n, k):
# breaks down the calculation into easily
# understood parts
numerator = factorial(n)
denominator = factorial(k) * factorial(n - k)
ways = numerator / denominator
return ways
# printGreeting() prints an explanation of the
# program for the user
# Inputs: None
# Outputs: None
def printGreeting():
print
print "This program will calculate the numbers of distinct ways"
print "to choose k objects from a set of n objects, otherwise known"
print "in math as C(n,k) or n choose k"
print
def main():
printGreeting()
# get input for n and k from the user
n = input("Enter number of objects in the set (n)? ")
k = input("Enter number to be chosen (k)? ")
# calculate and display ways to choose k from n
print "C(%d, %d) = %d" % (n, k, combinations(n, k))
main()
The Sample Run
linux3[72] % python combine.py This program will calculate the numbers of distinct ways to choose k objects from a set of n objects, otherwise known in math as C(n,k) or n choose k Enter number of objects in the set (n)? 6 Enter number to be chosen (k)? 2 C(6, 2) = 15 linux3[73] % !p python combine.py This program will calculate the numbers of distinct ways to choose k objects from a set of n objects, otherwise known in math as C(n,k) or n choose k Enter number of objects in the set (n)? 3 Enter number to be chosen (k)? 2 C(3, 2) = 3 linux3[74] % !p python combine.py This program will calculate the numbers of distinct ways to choose k objects from a set of n objects, otherwise known in math as C(n,k) or n choose k Enter number of objects in the set (n)? 12 Enter number to be chosen (k)? 4 C(12, 4) = 495
The Lesson
The Program
# File: trace.py
# Author: Sue Evans
# Date: 9/29/09
# Section: All
# EMail: bogar@cs.umbc.edu
#
# This program illustrates local variables and is
# to be used to demonstrate the techniques of
# tracing a program by hand. The non-meaningful
# function and variable names are intentional,
# since they are not REALLY doing anything that
# is meaningful except teaching you to trace
# function calls
# geez() outputs values of local variables, a
# common technique for debugging programs
#
# Input: an arbitrary integer, c
# Output: returns c + 100
def geez (c):
a = c + 100
b = 2 * a
print "geez: a = %d, b = %d, c = %d" % (a, b, c)
return a
# foobar() outputs values of local variables, a
# common technique for debugging programs
#
# Input: an arbitrary integer, b
# Output: returns b + 1
def foobar (b):
a = geez (b)
b += 1
c = b
print "foobar: a = %d, b = %d, c = %d" % (a, b, c)
return c
def main():
a = 1
b = 2
c = 3
c = geez(a)
b = foobar(c)
print "main: a = %d, b = %d, c = %d" % (a, b, c)
main()
The Sample Run
linuxserver1.cs.umbc.edu[103] python trace.py geez: a = 101, b = 202, c = 1 geez: a = 201, b = 402, c = 101 foobar: a = 201, b = 102, c = 102 main: a = 1, b = 102, c = 101 linuxserver1.cs.umbc.edu[104]
# File: trace2.py # Author: Sue Evans # Date: 9/29/09 # Section: All # Email: bogar@cs.umbc.edu # # This program illustrates local variables and is # to be used to demonstrate the techniques of # tracing a program by hand. The non-meaningful # function and variable names are intentional, # since they are not REALLY doing anything that # is meaningful except teaching you to trace # function calls. # # Function header comments have been removed to save space def g(b): c = b + 7 a = c - 2 print "g: a = %d, b = %d, c = %d" % (a, b, c) return a def f(a): b = 2 * a + 5 c = g(b) print "f: a = %d, b = %d, c = %d" % (a, b, c) return c def main(): a = 0 b = 0 c = 0 a = f(b); c = g(a); print "main: a = %d, b = %d, c = %d" % (a, b , c) main()