











HW6 - Loops
due on Sunday, 3/18 before 11:59 PM
Sue Evans & Don Miner
Hit the space bar for next slide












Sue Evans & Don Miner
Hit the space bar for next slide
Choose a positive integer and repeatedly do the following:
if the number is 1, quit; if the number is even, cut it in half;
if the number is odd, multiply it by 3 and add 1.
For example, if you start with the number 17, you get the sequence:
17 52 26 13
40 20 10
5 16 8
4 2 1.
Generate the sequence from a starting number and you'll find the numbers go up and down like a hailstone in a cloud before it plummets to earth (e.g., when the value is one).
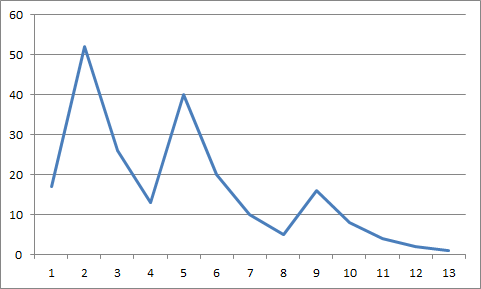
Does this procedure eventually reach 1 and stop for every choice
of starting number?
So far, this is an unsolved problem -- no one has proven that the process
always results in 1, and no one has found a counterexample. This problem
was first posed by L. Collatz in 1937 and goes under several names: the
Collatz conjecture, the '3n+1 conjecture', the Ulam
conjecture, and the Syracuse problem. The sequence is also commonly called
the hailstone sequence.
John Conway proved that the original Collatz problem has no nontrivial cycles of length less than 400. Lagarias (1985) showed that there are no nontrivial cycles with length less than 275,000. Conway (1972) also proved that Collatz-type problems can be formally undecidable. The conjecture has been check by computer for all start values up to 1.2 x 1012, but a proof of the conjecture has not been found. Paul Erdos said about the Collatz conjecture: "Mathematics is not yet ready for such problems." He offered $500 for its solution. There are some heuristic, statistical arguments supporting the conjecture: if one considers only the odd numbers in the sequence generated by the Collatz process, then one can argue that on average the next odd number should be about 3/4 of the previous one, which suggests that they eventually hit the bottom.
The problem:
The following iterative sequence is defined for the set of positive
integers:
n -> n/2 (if n is even)
n -> 3n + 1 (if n is odd).
Using the rule above and starting with 13, we generate the following
sequence:
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
The steps to generate the following sequence are as follows:
The following iterative sequence is defined for the set of
positive integers:
n -> n/2 (if n is even)
n -> 3n + 1 (if n is odd).
For this homework you are to write a program that prints out the chains for the numbers within a range that the user specifies. The length of each chain should be printed at the end of the chain.
For example, the line of output for 13 will look like:
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
This program should be menu driven. The user gets to choose to see one individual chain, to see all of the chains for a range of numbers, to see which number in a range had the longest chain, or to quit the program.
linuxserver1.cs.umbc.edu[101] python hw6.py
This program finds hailstone sequences of numbers you choose.
The next number in the hailstone sequence is found by dividing
the number in half if it's even and multiplying by 3 and adding
one if it is odd.
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : i
Enter a number (1-10000): 13
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : I
Enter a number (1-10000): 13
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : r
Enter the starting number (1-10000): 10
Enter the ending number (11-10000): 20
10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 7
11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -
> 4 -> 2 -> 1 ; length = 15
12 -> 6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
14 -> 7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10
-> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 18
15 -> 46 -> 23 -> 70 -> 35 -> 106 -> 53 -> 160 -> 80 -> 40 -> 20 -> 1
0 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 18
16 -> 8 -> 4 -> 2 -> 1 ; length = 5
17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 ->
1 ; length = 13
18 -> 9 -> 28 -> 14 -> 7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 21
19 -> 58 -> 29 -> 88 -> 44 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13
-> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 21
20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 8
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : l
Enter the starting number (1-10000): 1
Enter the ending number (2-10000): 100
97 had the longest chain 119
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : a
a is not a valid choice
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : r
Enter the starting number (1-10000): 3
Enter the ending number (4-10000): 2
Enter the ending number (4-10000): 10001
Enter the ending number (4-10000): 6
3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 8
4 -> 2 -> 1 ; length = 3
5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 6
6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 9
I - view sequence for an Individual value
R - view sequence for a Range of values
L - find the Longest chain
Q - Quit
Enter your choice : q
linuxserver1.cs.umbc.edu[102]
First, write a function hailstone() that contains a while loop that prints out a single chain and keeps track of how long it is. Each step of the while should move the current value to the next step.
You should make use of the isOdd(n) function that you wrote for
HW5 to check to see if it is odd.
Then change the number according.
Use a counter to keep track of the length of the chain. We did a similar thing with averages in lecture.
Test this function on 13 to make sure it works properly.
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 ; length = 10
Then, imbed a call to your hailstone function inside a for loop to print the chains from 10 to 20. Remember to use range.
Test this to make sure your program is giving output for all of the numbers in the range.
Next, get a copy of getValidInt() from the loops lecture, the Menu example slide. Use this to allow the user to to choose any starting and stopping numbers they want instead of 10 to 20. Since your hailstone() function prints output to the screen, you'll want to restrict the user's range to values between 1 and 10000 (printing output takes up a lot of time). The ending number of the range needs to be more than the starting number, as it was in HW5.
Test this on the values 10 to 20. See if you get the same results.
At this point you have written the code necessary to do two of the three hailstone tasks, so let's work on the menu next. Use parts of the menu example, rectangle.py from the loops lecture as a guide/template for coding a working menu.
Test your menu for the individual value 13, and the range of values 10 to 20. See if your menu works properly.
Implement the last hailstone task: find the longest chain in a range. Your hailstone() function will now have to return the length. If you aren't doing the extra credit and plan to print all of the chains as well as the result, restrict the user to 1 - 10000.
Test this choice to make sure it works properly.
Test your menu to make sure it rejects bad input and quits when it should.
Then, write the printGreeting() function and call it. Test this too.
Finally, write your file header comment and your function header comments if you haven't already done so. Hopefully, you did your inline comments while you were writing the code.
Test all of the functionality again before you submit your file.
Which starting number, under one million, produces the longest chain?
In order for your program to run in a reasonable amount of time, don't print out each chain, just print out which one is the longest and how long it is. This should be a modification of choice L to be in the range 1 - 1000000 and it should only print the result. Don't think this is going to take a long time to run. It should finish in about 70 seconds.
You should add another menu choice for this, X, for extra credit.
After you've finished your assignment, use the submit command to turn it in.
submit cs201 HW6 hw6.py
Don't forget to watch for the confirmation that submit worked correctly.
Specifically, the confirmation will say:
Submitting hw6.py...OK
If not, try again.
You can check your submission by entering
submitls cs201 HW6
You should see the name of the file that you just submitted,
in this case, hw6.py.