











Introduction to Recursion
Sue Evans & Will Murnane
Hit the space bar for the next slide












Sue Evans & Will Murnane
Hit the space bar for the next slide
We have concentrated on top-down design and the use of functions so far in this course. You certainly have no problems writing functions at this point, but we still haven't examined all of the usefulness of functions.
You are quite aware that functions can call other functions, like this :
>>> def alpha(name):
... print "Function alpha called with argument", name
...
>>> def beta(foo):
... print "Function beta starting with argument", foo
... alpha(foo)
...
>>> beta("Hello, World!")
Function beta starting with argument Hello, World!
Function alpha called with argument Hello, World!
Functions aren't limited to calling functions with other names; they can also call themselves. Suppose we wanted to count down to some momentous occasion using a function. We could do this with a for or while loop, but for the sake of trying something new, let's try to implement this with a function that calls itself. Here's a first attempt:
>>> def countdown(n): ... print n ... countdown(n-1) ... >>> countdown(10) 10 9 8 7 6 5 4 3 2 1 0 -1 -2 -3 (much more output) File ">stdin<", line 3, in countdown File ">stdin<", line 3, in countdown File ">stdin<", line 3, in countdown File ">stdin<", line 3, in countdown RuntimeError: maximum recursion depth exceeded
Uh-oh. Something's wrong.
Let's look deeper to try to figure out what happened and how to fix it.
We'll come back to this example in a few slides.
Let's try tracing through a program that has some function calls in it and see what the execution stack would look like at each stage.
>>> def one(): ... two() ... three() ... >>> def two(): ... four() ... print "Done with two()" ... >>> def three(): ... print "Almost done" ... >>> def four(): ... print "Hello from four()!" ... >>> one()
So we start with just one entry on the stack, which we'll call "interpreter". After all, after one() finishes executing, we'll be back in the interpreter. So, here's the stack right as we enter one():
The next thing we do in one is call two(). So where we are is pushed onto the top of the stack:
Again, we immediately execute a function call in two, so where we are now is pushed onto the stack:
Now we're in four, so we print the message "Hello from four()!". Now it's time to return from four, so we pop the first entry off the top of the stack and go to that address. Now we're back in two , and let's see the stack now.
So before we started with the function call, we were on line 1 of two. Now we'll move on to the next thing in two, which is a print statement again. We print the message, and we're ready to return from two. We take the pop the stack again and go to that address. Now we're in one, done with line 1 and about to execute line 2, and the stack contains only
Then we have to call three, so we push our current location onto the stack:
Now we print the message in three and return to one. Since there's nothing left in one, we return one final time to the interpreter.
Our earlier program
>>> def countdown(n): ... print n ... countdown(n-1) ...
complained about "maximum recursion depth exceeded". What happened here is we just kept calling functions (namely, countdown) until the size of the stack got too big to deal with and Python complained. countdown also has one fatal flaw: it kept counting even when the number was less than zero. This is one of the most important things to keep in mind with recursion:
We must define the base case. This is the name given to the conditions under which the recursion stops.
In this case, when n reaches zero we want to print some kind of message. So we'll check for this condition before calling countdown again:
>>> def countdown(n): ... if n <= 0: ... print "Blastoff!" ... return ... print n ... countdown(n-1) ...
Now we execute this code, and the result is as expected:
>>> countdown(10) 10 9 8 7 6 5 4 3 2 1 Blastoff!
A recursive definition is one which refers to itself as in these definitions of the factorial and fibonacci functions.
n! or fact(n) is defined as:
fact(0) = 1
fact(n) = n * fact(n-1) , for n > 0
the nth fibonacci number or fib(n) is defined as:
fib(0) = 1
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2) , for n > 1
A recursive function is a function that calls itself.
def factorial (n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
Eventually the problem can be reduced to one of the simple solutions.
Leonardo Pisano Fibonacci, the Italian mathematician, is famed for his invention of the fibonacci sequence -- 1,1,2,3,5,8,13,21,34,... -- where each number is the sum of the previous two. The sequence appears in his work known as the "rabbit problem":
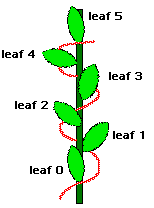
The arrangement of leaves or twigs on a stem (phyllotaxis, from the Greek word phyhllon meaning leaf and taxis meaning arrangement) correspond to Fibonacci numbers. Select one leaf as a starting point and count up the leaves on the stem until you reach a leaf directly above your starting point. The number of leaves is usually a Fibonacci number. In the above figure, starting from the bottom leaf, we count up 5 leaves to find the next one directly above the bottom leaf. Also, you can count the number of turns around the stem, as you go from a leaf to one directly above it. This too is usually a Fibonacci number. For a pussy willow, typical numbers are 13 for the number of "leaves" and 5 times around.
Many web sites have fascinating discussions about Fibonacci Numbers in Nature. This is a particularly good one from World-Mysteries.
fib(n) = undefined for n < 0 fib(0) = fib(1) = 1 fib(n) = fib(n-1) + fib(n-2) for n > 1
def fib(n):
# base case
if n < 2:
return 1
# general rule
else:
return fib(n - 1) + fib(n - 2)
def fib(n):
f1 = 1
f2 = 1
if n < 2:
return 1
else:
for i in range(2, n):
temp = f1
f1 = f2
f2 = temp + f2
return (f1 + f2)
A recursive function for fibonacci with tracing.
# File: fib1.py
# Author: Richard Chang
# Date: 12/3/97
# Modified by Sue Evans - 11/19/09
# Section: All
# EMail: bogar@cs.umbc.edu
#
# A recursive function for fibonacci with tracing.
# fib() recursively traces the fibonacci sequence
# for the nth number in the sequence
#
# Input: the number-place in the sequence to find
# Output: the value of the nth number in the sequence
# Side effect: prints tracing for finding the number
def fib(n):
print "> fib(%d)" % (n)
if n < 2:
result = 1
else:
result = fib(n - 1) + fib(n - 2)
print "< %d" % (result)
return result
def main():
n = -1
while n < 1:
n = input("Enter a positive integer: ")
fib(n)
main()
linuxserver1.cs.umbc.edu[111] python fib1.py Enter a positive integer: 4 > fib(4) > fib(3) > fib(2) > fib(1) < 1 > fib(0) < 1 < 2 > fib(1) < 1 < 3 > fib(2) > fib(1) < 1 > fib(0) < 1 < 2 < 5 linuxserver1.cs.umbc.edu[112]
Wow! I can't really see what's going on.
A recursive function for fibonacci with indented tracing.
# File: fib2.py
# Author: Richard Chang
# Date: 12/3/97
# Modified by Sue Evans - 11/19/09
# Section: All
# EMail: bogar@cs.umbc.edu
#
# A recursive function for fibonacci with indented tracing.
# indent() prints vertical lines for the depth of
# recursion in a recursive function to be traced
#
# Input: depth, will be the number of lines
# Output: [depth] printed lines, no return value
def indent(depth):
for i in range(depth):
print "| ",
# fib() recursively traces the fibonacci sequence
# for the nth number in the sequence
#
# Input: the number-place in the sequence to find
# Output: the value of the nth number in the sequence
# Side effect: prints tracing for finding the number
def fib(n, depth):
indent(depth)
print "> fib(%d)" % (n)
if n < 2:
result = 1
else:
result = fib(n - 1, depth + 1) + fib(n - 2, depth + 1)
indent(depth)
print "< %d" % (result)
return result
def main():
n = -1
while n < 1:
n = input("Enter a positive integer: ")
fib(n, 0)
main()
Let's see if this helped!
linuxserver1.cs.umbc.edu[118] python fib2.py Enter a positive integer: 4 > fib(4) | > fib(3) | | > fib(2) | | | > fib(1) | | | < 1 | | | > fib(0) | | | < 1 | | < 2 | | > fib(1) | | < 1 | < 3 | > fib(2) | | > fib(1) | | < 1 | | > fib(0) | | < 1 | < 2 < 5 linuxserver1.cs.umbc.edu[119]
This is still pretty hard to understand. Let's trace it by hand!
Realize that multiplication is simply repeated adding.
When we say a * b,
we mean to add a to its previous sum b times
Write a recursive function called multiply() that does multiplication by repeated adding.
 The Towers of Hanoi is a puzzle consisting of three pegs, and a number
of discs of different sizes which can fit onto any peg.
The Towers of Hanoi is a puzzle consisting of three pegs, and a number
of discs of different sizes which can fit onto any peg. There is a backstory involving Zen monks and 64 golden discs, but it's invented.

Let's think about a recursive algorithm for solving the Towers of Hanoi
Preliminaries
For a start, let's consider a small number of discs: two.
To move these two discs from A to C:
we move the first disc from A to B,
then move the second disc from A to C,
then move the first disc from B to C.
To solve the Towers of Hanoi problem of size n with the intermediate peg "spare", moving the discs from "src" to "dest":
Translating this into the language of the original problem it becomes:
To move n discs from peg A to peg C:
Based on this algorithm, we can define the hanoi() function
# File: hanoi.py
# Author: Will Murnane
# Modified by: Sue Evans
# Date: 11/19/09
# Section: All
# Email: bogar@cs.umbc.edu
#
# This program solves the Towers of Hanoi puzzle
# using recursion
# move() prints the move from source to destination
#
# Inputs: src, the source peg
# dest, the destination peg
# Output: None
def move(src, dest):
print 'move ' + str(src) + '-->' + str(dest)
# hanoi() recusively solves the Towers of Hanoi problem
# for any positive n > 1
#
# Inputs: n, the number of discs
# dest, the destination peg
# src, the source peg
# spare, the extra peg
# Output: None
def hanoi(n, dest, src, spare):
# the base case
if n == 0:
return
# the general rule
hanoi(n - 1, spare, src, dest)
move(src, dest)
hanoi(n - 1, dest, spare, src)
def main():
discs = -1
while discs != 0:
discs = input("Enter the number of rings (0 to end): ")
hanoi(discs, 'C', 'A', 'B')
main()
Let's watch it run!
linuxserver1.cs.umbc.edu[132] python hanoi.py Enter the number of rings (0 to end): 2 move A-->B move A-->C move B-->C Enter the number of rings (0 to end): 3 move A-->C move A-->B move C-->B move A-->C move B-->A move B-->C move A-->C Enter the number of rings (0 to end): 0 linuxserver1.cs.umbc.edu[133]
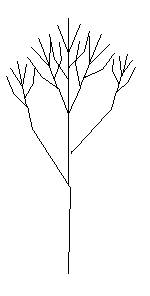
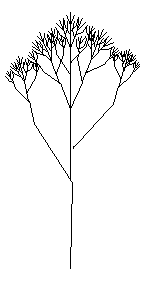
A fractal is a geometric object which can be divided into parts, each of which is similar to the original object.
A Koch snowflake is a simple example.
It's the result of infinite additions of triangles to the perimeter of a starting triangle.
Each time new triangles are added (an iteration), the perimeter grows, and eventually approaches infinity.
In this way, the fractal encloses a finite area within an infinite perimeter.
A complex fractal shape emerges from the simple repetition of a basic shape at a smaller and smaller scale.
When you zoom in to a fractal, at every scale it appears the same.
If you "zoom in" on the infinite version of a Koch curve, you see more and more detail, but it all looks the same.
Here's an animation:

Self-similarity makes fractals useful for modeling natural systems.
Consider the shape of a tree. From the trunk of a tree shoot off several branches.
Each branch then repeats this branching pattern and gives rise to smaller branches.
So the tree branching is self-similar.
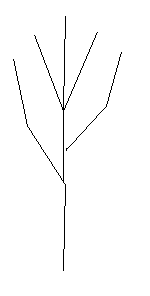 |
 |
 |
some material adapted from MathBlues
Anagrams are popular puzzles where a jumbled word is shown and the player tries to find all of the words that are possible from those letters.
We're going to write an anagram solving program. We'll ask the user to enter a word or a jumbled word and we'll create all permutations of those letters and check the linux dictionary to see if any of those permutations are actually a word.
| Length of Word | Number of Permutations |
|---|---|
Here's anagrams.py
# Filename: anagrams.py
# Author: Sue Evans
# Date: 11/22/09
# Section: All
# Email: bogar#cs.umbc.edu
#
# This program recursively generates all possible permutations
# of a 6-letter or less jumbled word entered by the user, then
# searches the dictionary using a recursive binary search for
# possible solutions.
import sys
import string
MAX_LEN = 6
NUM_ARGS = 2
# anagrams() recursively produces a set of all possible
# permutations of the word passed in.
#
# Input: str, the word
# Output: answer, the list of permutations
def anagrams(str):
# base case 1
if str == "":
return [str]
else:
answer = []
# general case
# call anagrams passing all but the 1st letter
for word in anagrams(str[1:]):
for pos in range(len(word) + 1):
answer.append(word[:pos] + str[0] + word[pos:])
# base case 2
return answer
# getDictList() reads in all of the words in the
# dictionary file, strips them of trailing whitespace
# and changes them to all lower-case
#
# Input: filename, the path and filename of the dictionary file
# Output: dictWords, the list of dictionary words
def getDictList(filename):
dictWords = []
dictFile = open(filename, 'r')
for line in dictFile:
str = string.strip(line)
str = string.lower(str)
dictWords.append(str)
dictFile.close()
return dictWords
# binarySearch() searches recursively for an item in a list using
# the binary search algorithm.
#
# Inputs: item, the item to be searched for
# list, the list to search
# left, the left index
# right, the right index
# Output: found, the index where item occurred in list or -1 if not found
def binarySearch(item, list, left, right):
# base case 1
# no place left to look - not there
if left > right:
return -1
mid = (left + right) / 2
str = list[mid]
# base case 2
# if item was found stop looking
if str == item:
return mid
# general rule
# look in lower half
elif item < str:
return binarySearch(item, list, left, mid - 1)
# look in upper half
else:
return binarySearch(item, list, mid + 1, right)
def main():
# Check for correct number of command-line arguments
argc = len(sys.argv)
if argc != NUM_ARGS:
print "This program requires a command line argument which is"
print "the path to the linux dictionary"
print "Useage: anagrams.py /usr/share/dict/words"
sys.exit()
# Get a word from the user that is less than
# or equal to MAX_LEN characters
word = ""
while(len(word) < 1 or len(word) > MAX_LEN):
word = raw_input("Enter a jumbled word of 6 or less characters : ")
# Strip it of trailing whitespace & make it all lower-case
word = string.strip(word)
word = string.lower(word)
# Get a list of all permutations of the word
perms = anagrams(word)
num = len(perms)
# Get a list of the words in the dictionary file
dictWords = getDictList(sys.argv[1])
dictLen = len(dictWords)
# Search the dictionary for each of the permutations
# printing those that are actually words
for i in range(num):
found = binarySearch(perms[i], dictWords, 0, dictLen - 1)
if found != -1:
print perms[i]
main()
Let's run it!
linuxserver1.cs.umbc.edu[204] python anagrams.py /usr/share/dict/words Enter a jumbled word of 6 or less characters : eap ape epa pea linuxserver1.cs.umbc.edu[205] python anagrams.py /usr/share/dict/words Enter a jumbled word of 6 or less characters : lenag nagle nagel lange angle angel lagen agnel genal elgan glean galen