Computer systems are constructed of digital electronics. That means that their electronic circuits can exist in only one of two states: on or off. Most computer electronics use voltage levels to indicate their present state. For example, a transistor with five volts would be considered "on", while a transistor with no voltage would be considered "off." Not all computer hardware uses voltage, however. CD-ROM's, for example, use microscopic dark spots on the surface of the disk to indicate "off," while the ordinary shiny surface is considered "on." Hard disks use magnetism, while computer memory uses electric charges stored in tiny capacitors to indicate "on" or "off."

These patterns of "on" and "off" stored inside the computer are used to encode numbers using the binary number system. The binary number system is a method of storing ordinary numbers such as 42 or 365 as patterns of 1's and 0's. Because of their digital nature, a computer's electronics can easily manipulate numbers stored in binary by treating 1 as "on" and 0 as "off." Computers have circuits that can add, subtract, multiply, divide, and do many other things to numbers stored in binary.

The decimal number system that people use every day contains ten digits, 0 through 9. Start counting in decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Oops! There are no more digits left. How do we continue counting with only ten digits? We add a second column of digits, worth ten times the value of the first column. Start counting again: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 (Note that the right column goes back to zero here.), 21, 22, 23, ... , 94, 95, 96, 97, 98, 99, Oops! Once again, there are no more digits left. The only way to continue counting is to add yet another column worth ten times as much as the one before. Continue counting: 100, 101, 102, ... 997, 998, 999, 1000, 1001, 1002, .... You should get the picture at this point.

Another way to make this clear is to write decimal numbers in expanded notation. 365, for example, is equal to 3×100 + 6×10 + 5×1. 1032 is equal to 1×1000 + 0×100 + 3×10 + 2×1. By writing numbers in this form, the value of each column becomes clear.

The binary number system works in the exact same way as the decimal system, except that it contains only two digits, 0 and 1. Start counting in binary: 0, 1, Oops! There are no more binary digits. In order to keep counting, we need to add a second column worth twice the value of the column before. We continue counting again: 10, 11, Oops! It is time to add another column again. Counting further: 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.... Watch the pattern of 1's and 0's. You will see that binary works the same way decimal does, but with fewer digits.

Binary uses two digits, so each column is worth twice the one before. This fact, coupled with expanded notation, can be used convert between from binary to decimal. In the binary system, the columns are worth 1, 2, 4, 8, 16, 32, 64, 128, 256, etc. To convert a number from binary to decimal, simply write it in expanded notation. For example, the binary number 101101 can be rewritten in expanded notation as 1×32 + 0×16 + 1×8 + 1×4 + 0×2 + 1×1. By simplifying this expression, you can see that the binary number 101101 is equal to the decimal number 45.

An easy way to convert back and forth from binary to decimal is to use Microsoft Windows Calculator. You can find this program in the Accessories menu of your Start Menu. To perform the conversion, you must first place the calculator in scientific mode by clicking on the View menu and selecting Scientific mode. Then, enter the decimal number you want to convert and click on the "Bin" check box to convert it into binary. To convert numbers from binary to decimal, click on the "Bin" check box to put the calculator in binary mode, enter the number, and click the "Dec" check box to put the calculator back in decimal mode.

Binary is an effective number system for computers because it is easy to implement with digital electronics. It is inefficient for humans to use binary, however, because it requires so many digits to represent a number. The number 76, for example, takes only two digits to write in decimal, yet takes seven digits to write in binary (1001100). To overcome this limitation, the hexadecimal number system was developed. Hexadecimal is more compact than binary but is still based on the digital nature of computers.

Hexadecimal works in the same way as binary and decimal, but it uses sixteen digits instead of two or ten. Since the western alphabet contains only ten digits, hexadecimal uses the letters A-F to represent the digits ten through fifteen. Here are the digits used in hexadecimal and their equivalents in binary and decimal:

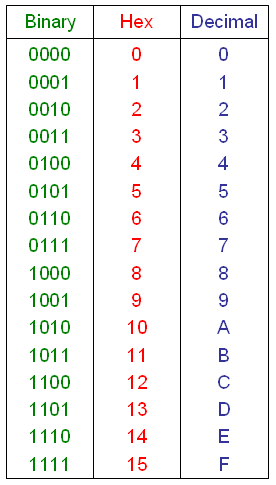
Let's count in hexadecimal. Starting from zero, we count 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. At this point there are no more digits, so we add another column. Continue counting: 10, 11, 12, 13, 14, 15, 16, 17 18, 19, 1A, 1B, 1C, 1D, 1E, 1F. Once again, we are out of digits in the first column, so we add one to the next column. Continue counting once again: 20, 21, 22, ..., 29, 2A, 2B, 2D, 2E, 2F, 30, 31, 32, ..., 3E, 3F, 40, 41, 42, ... 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2, ... F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, .... Watch the pattern of numbers and try to relate this to the way you count in decimal or binary. You will see that it is the same procedure, but with sixteen digits instead of 10 or 2.

Each column in hexadecimal is worth 16 times the column before, while each column in binary is worth 2 times the column before. Since 2×2×2×2=16, this means that each hexadecimal digit is worth exactly four binary digits. This fact makes it easy to convert between binary and hexadecimal.

To convert from hexadecimal to binary, simply look at the chart above and replace each digit in the hexadecimal number with its corresponding four-digit binary number. For example, 8F in hexadecimal is 10001111 in binary, since 8=1000 and F=1111.

To convert from binary to hexadecimal, reverse the procedure and break the binary number into blocks of four digits. Then, replace each block of four digits with its corresponding hexadecimal digit. If you cannot divide the binary number evenly into blocks of four digits, add zeros to the left side of the number to make it work. For example, to convert 110101 to hexadecimal, first add two zeros at the beginning of the number to make it 00110101. Since 00110101 has eight digits, it can be divided into two blocks of four digits, 0011 and 0101. Since 0011=3 and 0101=5, the corresponding hexadecimal number is 35.