CMSC-341 Spring 2001
Project 5
| Assigned |
Monday 30 April, 2001 |
| Preview Sessions |
Wed 01 May 20001
Thurs 02 May 2001 |
| Due |
Midnight, Sunday 13 May 2001 |
Background
Graphs can be applied to many real world applications from computer networks
to UPS truck routing and many things in-between. This project will
allow you apply what you've learned about graph implementation and graph
related algorithms to solving a real problem. You will be completing
a modified version of exercise 9.45 from the textbook, found on page 384.
Description
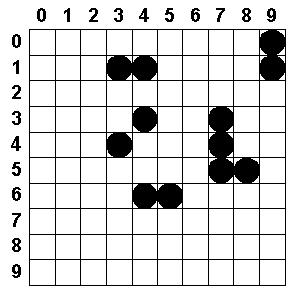
Consider an N x N grid (like a checker board) in which
some of the squares are occupied by black circles (representing checkers).
Two squares in the grid belong to the same group if they share a common
edge. Squares are designated by the ordered pair (row, column).
For example, squares (0, 0) and (0,1) are in the same group as are (0,
0) and (1, 0). However, squares (0, 0) and (1, 1), are not in the
same group. In the figure below, there is one group of four occupied
squares, three groups of two occupied squares and two individual occupied
squares ("groups" of one). Your mission is to write a program that
does the following:
-
Opens and reads the grid description file
-
Creates an appropriate undirected graph representing the occupied squares
-
Prints the grid in the format specified in the sample
output below
-
Identifies and lists all of the occupied groups in the grid
Project requirements
-
Think about this project before you start coding. One
of the challenges of this project is to design a way to properly "translate"
between the external view of the data (row/column pairs) and a more generic
internal representation of the vertices and edges. This type of translation
is a fundamental problem in design objects and writing code that solves
real world problems.
-
The size of the grid will be read from the grid description
file. You may use either the adjacency table or adjacency list for
your graph representation (your choice). However, because the size
of the graph is determined at runtime, you must use the vector<T>
class (provided by the text and available in Mr. Frey's public directory)
to hold the graph data.
-
Your graph must be implemented as a class template,
as will your vertex class. Otherwise, you are free to design whatever
other classes you deem necessary.
-
The Graph class may be a friend of the Vertex class.
No other friendship is permitted between classes or between functions and
classes.
-
Your executable MUST be named Proj5
and your makefile must be named makefile
or Makefile. Otherwise you are free
to name your files as you wish, but there must be one .H and one .C file
per class.
ADT Descriptions
The Vertex ADT
Since a vertex may contain data of any kind, your vertex
must be a class template. Your vertex should also hold information
(i.e. vertex number) that is internal and known only to the Graph.
You'll find it much easier to use this internal vertex number to identify
vertices and edges in the Graph.
Like List nodes and Tree nodes, the vertices of
a graph are only known to and only manipulated by the Graph class. Therefore
all data and all methods of the Vertex class must be private. You
make may the Graph a friend of the Vertex for easier coding. You
may create whatever methods and data you feel necessary.
The Graph ADT
Like Lists and Trees, Graphs can hold any kind of data
(in the vertices). Therefore, the Graph class must be a template.
You should implement your graph for this project as an undirected graph.
The Graph class must support the following public operations.
The nature of the vertices used as parameters is purposefully missing.
You are at liberty to specify the method parameters and return types.
-
The Big-4
-
addVertex ( ) -- adds a vertex to the graph containing the
data to be stored in the graph
-
addEdge ( ) -- adds an undirected edge to the graph
between two specified vertices
-
listComponents ( ) -- prints a list of the connected components
as specified in the project description
In addition, you may support any of the following
operations found in the graph notes and discussed in class as either public
or private methods.
-
getDegree ( ) -- returns the degree of specified vertex
-
getAdjacent ( ) -- returns a list of vertices adjacent from the specified
vertex
-
isConnected ( ) -- returns TRUE if the two specified vertices are connected,
FALSE otherwise
Other objects
You may want to create other object(s) as well for this
project (an object to hold the data found in the vertex, for example).
You are free to specify the ADT for these objects as necessary provided
that you provide the Big-4 and all data is private.
Grid Description File Format
The grid data file has the following format:
-
The first line of the file contains a single integer which is the size
of the square grid
-
All remaining lines in the file contain two integers separated by a space.
These are the zero based row and column of the occupied squares, respectively.
You may assume that all row and column values are valid, but no order is
guaranteed.
The grid description file for the figure above can be found in Mr. Frey's
public directory
/afs/umbc.edu/users/d/e/dennis/pub/CMSC341/Proj5
Sample Output
The grid should be printed using the following symbols:
-
A dash (or hyphen) is used to represent unoccupied squares
-
A capital "O" is used to represent occupied squares
Rows and columns must be labeled and start at zero
The figure above would be output as
0 1 2 3 4 5 6 7 8 9
0 - - - - - - - - - O
1 - - - O O - - - - O
2 - - - - - - - - - -
3 - - - - O - - O - -
4 - - - O - - - O - -
5 - - - - - - - O O -
6 - - - - O O - - - -
7 - - - - - - - - - -
8 - - - - - - - - - -
9 - - - - - - - - - -
The occupied groups are identified by listing the
squares in the group. For the figure above, the output would be
Group 1: (0, 9), (1, 9)
Group 2: (1, 3), (1, 4)
Group 3: (3, 4)
Group 4: (4, 3)
Group 5: (3, 7), (4, 7), (5, 7),
(5, 8)
Group 6: (6, 4), (6, 5)
Your output does not have to be formatted exactly the same, but squares
must be designated as (row, column).
Groups may be listed in any order and squares within a group may be
listed in any order.
Vector Files
The source code files vector.C and vector.H are available in Mr. Frey's
public directory
/afs/umbc.edu/users/d/e/dennis/pub/CMSC341.
As in earlier projects, DO NOT copy these files to your directory
and DO NOT submit the vector files. Your makefile should specify
these files where appropriate.
Files To Be Submitted
You should submit only the files you have written, a makefile, and the
file containing your answers to the questions. The files to be submitted
are:
-
Definition (.H) and implementation (.C) files for your graph class
-
Definition (.H) and implementation (.C) files for your graph node class
-
Proj5.C
-
Your makefile
-
A copy of the question file that contains your answers
-
A readme file for the grader if you think you deserve extra credit
If your makefile is set up correctly, you should be able to execute the
command make submit.
Questions
Copy the file /afs/umbc.edu/users/d/e/dennis/CMSC341/Proj5/341-Spring01-proj5_questions.txt
to
your directory, then edit the file to add you answers. Be sure to
submit your file.
Grading and Academic Integrity
Project grading is described in the Project
Policy handout.
Your answers to 341-Spring01-proj5_questions.txt
are worth 10% of your project grade.
Cheating in any form will not be tolerated. Please re-read the Project
Policy handout for further details on honesty in doing projects for
this course.
Remember, the due date is firm. Submittals made after midnight of the
due date will not be accepted. Do not submit any files after that time.
Last modified on Friday, April 27, 2001 by Dennis Frey
email: frey@cs.umbc.edu