CMSC 341 - Fall 1998 -- Final Exam Review
- Define "Big-Oh"
- Number these functions in ascending "Big-Oh" order
O(n2), O(n lg n), O(1), O(lg0.1 n), O(2n), O (lg n), O(sqrt(n))
- Prove O(cf(x)) = O(f(x))
- Suppose T1(n) = O(f(n)) and T2(n) = O(f(n)).Prove that T1(n) + T2(n) = O(f(n))
- Define the following
- graph
- directed graph
- undirected graph
- weighted graph
- directed acyclic graph
- topological ordering of a directed acyclic graph
- minimum spanning tree of a weighted graph
- connected, undirected graph
- strongly connected directed graph
- weakly connected directed graph
- Prove that in any undirected graph, |E| = O(|V|2)
- Write pseudo-code for breadth-first and depth-first traversals of undirected graphs. The code must be complete and fully describe the operations.
- Let G = (V, E) be an undirected graph with V the set of vertices and E
the set of edges.
Let v1, v2, . . . Vp be all the members
of V and let q = |E|, the cardinality of E.
Prove that the sum of the degrees of all vertices = 2q.
- Describe any adjacency table implementation for a graph. How does it differ for directed and undirected graphs?
- Describe any adjacency list implementation for a graph. How does it differ for directed and undirected graphs?
- Briefly describe the adjacency table and adjacency list implementations of a graph -- include advantages and disadvantages; describe the asymptotic worst-case storage requirements for each and describe
the worst-case asymptotic performance of the operations below.
Note that u and v are vertices in the graph.
Degree(u) -- returns the degree of node u (undirected graph)
InDegree(u) -- returns the indegree of node u (directed graph)
OutDegree(u) -- returns the out-degree of node u (directed graph)
AdjacentTo(u) -- returns a list of nodes adjacent to node u
AdjacentFrom (u) -- returns a list of nodes adjacent from u
Connected (u, v) -- returns TRUE if there is an edge between u and v FALSE if not.
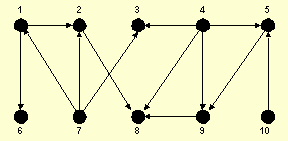
- Find a topological sorting for the given directed graph. Describe the
method you used and show all your work.
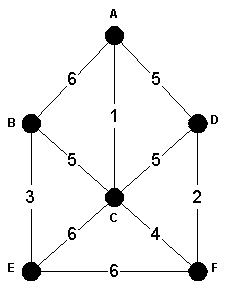
- Describe Prim's algorithm for generating a minimum-spanning tree in a weighted undirected graph. What is the "Big-Oh" performance of Prim's algorithm? Justify your answer.
- Describe Kruskal's algorithm for generating a minimum-spanning tree in a weighted, undirected graph. What is the Big-Oh performance of Kruskal's algorithm? Justify your answer.
- Find the minimum-spanning tree for the given weighted-undirected graph below using both Prim's and Kruskal's algorithm. Show your work.
- Define the single-source shortest path problem.
- Provide pseudo code for solving the single-source shortest path problem in an unweighted, connected undirected graph. What is the asymptotic performance of your algorithm? Justify your answer.
- Run Dijkstra's algorithm on the following directed graph to complete the table below, where d(v) is the distance from the source node to the vertex v; p(v) is the immediate predecessor of vertex v in the path from the source node to v.
Use vertex V1 as the source node.
What is the shortest distance and shortest path from V1
to V5?

|
Vertex |
D(v) |
P(v) |
|
V1 |
|
|
|
V2 |
|
|
|
V3 |
|
|
|
V4 |
|
|
|
V5 |
|
|
- Under what circumstances does Dijkstra's algorithm produce
incorrect
results for a weighted, directed graph? Give an example of such a graph.
- Define HEAP.
- State the Heap property. What implications does the heap property have for the values stored in the heap?
- Where are the largest, 2nd largest, 3rd largest and smallest elements located in a HEAP?
- Explain how to modify HeapSort to sort in descending order.
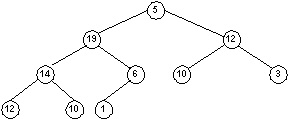
- Which node in the following "heap" violates the heap property?
Illustrate the calls to HEAPIFY () to restore the heap property.
- Define hash table, collision, separate chaining, linear probing, primary clustering, hash function
- Demonstrate the insertion of the keys 5, 28, 19, 15, 20, 33, 12, 17
and 10
into a hash table with collision resolved by chaining.
Let the table have 9 slots and let the hash function be h(k) = k mod
9.
- Illustrate the result of inserting the keys 10, 22, 31, 4, 15, 28, 17,
88 and 59 into a hash table of length 11 using open addressing with hash
function h(k) = k mod 11 by completing the table below, where each column shows the contents of the hash table
after inserting the value in the column heading.
|
Index |
Empty |
10 |
22 |
31 |
4 |
15 |
28 |
17 |
88 |
59 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|







