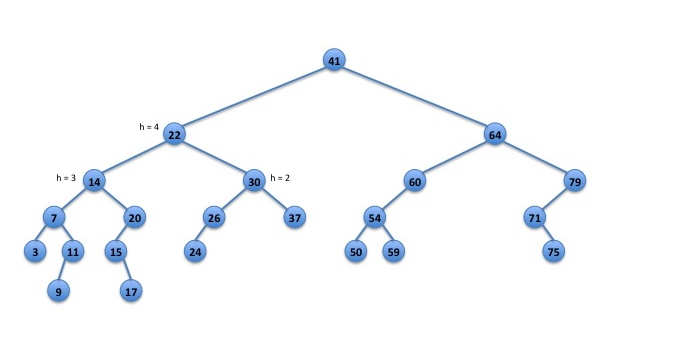
Fig. 1: an unbalanced binary search tree.
Figure 1 below, shows an example of an unbalanced binary search tree. At node 22, the left subtree has 8 nodes and the right subtree only has 4 nodes. If we encountered node 22 during an insert, we would invoke rebalance() on the subtree rooted at node 22. The subtree rooted at node 30 also has twice as many nodes in the left subtree than the right subtree. However, the height of node 30 is only 2. We will only rebalance subtrees of height 4 or higher. So, we will rebalance at node 22 but not at node 30.

Fig. 1: an unbalanced binary search tree.
After the first step of the rebalance() procedure, the left subtree of node 41 has been converted into an array, as shown in Figure 2, below:
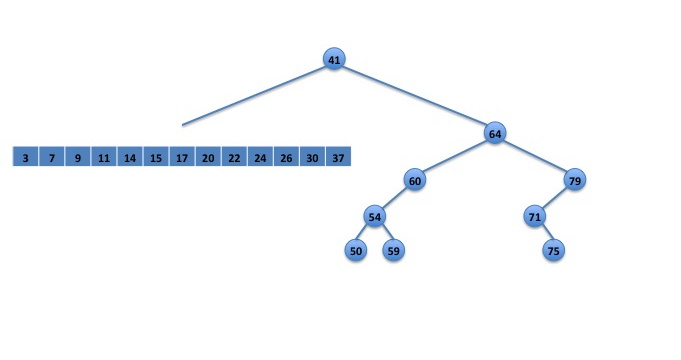
Fig. 2: subtree converted to an array.
When we rebuild the BST, we pick the middle element of the array, 17 in this case, and make it the root of the new subtree.
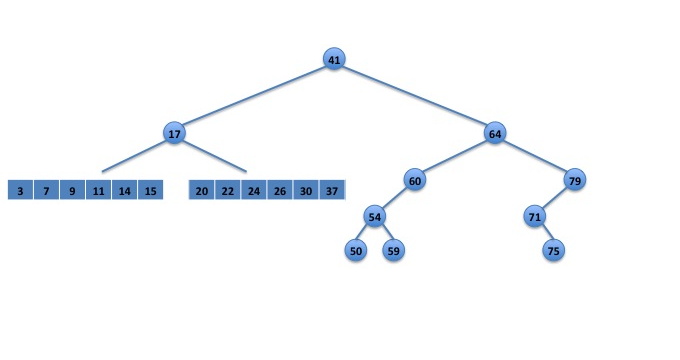
Fig. 3: 17 chosen as the root of the new subtree.
Items smaller than 17 are used to rebuild the left subtree of node 17. The items larger than 17 are used to rebuild the right subtree of node 17. The result is a BST that is as balanced as possible:
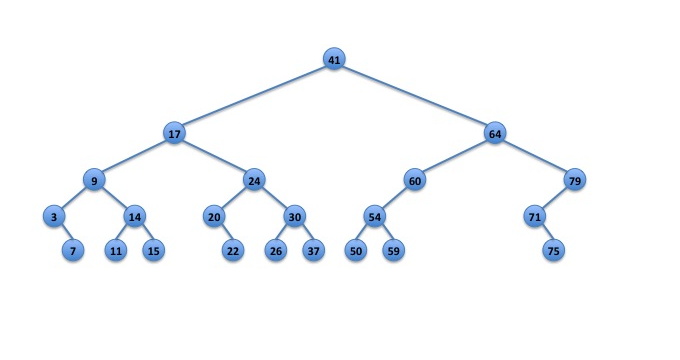
Fig. 4: array converted back to a lazy BST.
In Figure 5, there are two places where we can rebalance. Node 14 has height 4 and its right subtree has 4 items compared to 2 times in the left subtree. So, node 14 is a candidate for rebalance.
Similarly, node 22 has 7 nodes in the left subtree and 3 nodes in the right subtree. Thus, with height 5, node 22 is also a candidate for rebalance.
In this situation, we want to rebalance at node 22 and not at node 14, because when we rebalance node 22 we will also rebuild the subtree rooted at 14.
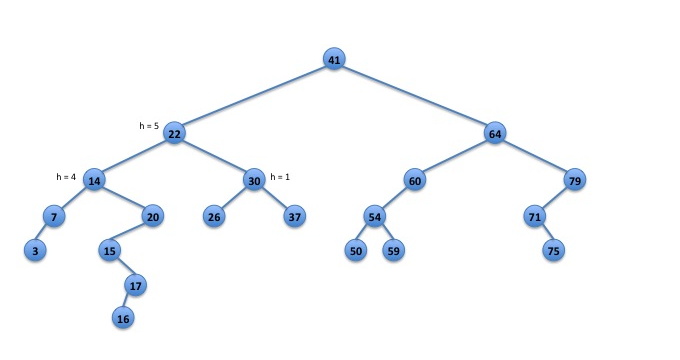
Fig. 5: subtree converted to an array.