Due: Tuesday, October 1, 11:59pm

Objectives

Introduction

For this project, you will implement a square list data structure. A square list is a linked list of linked lists where each linked list is guaranteed to have O(√n) items:

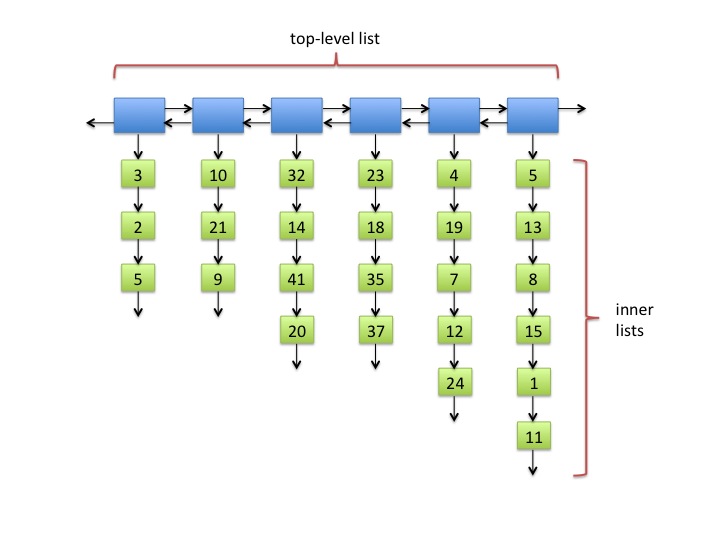
Fig. 1: A typical square list.

Figure 1 shows a typical square list of 25 integer values. The positions of the items are important. The ordering of the items in this example is: 3, 2, 5, 10, 21, 9, 32, 14, 41, 20, 23, ..., 15, 1, 11.

The idea of a square list is that we want to keep the length of the top-level and of all the inner lists bounded by O(√n). That way we can find the i^th item of the list in O(√n) time. For example, if we want to find the 9th item in the list, we can progress down the top-level list and check the length of the inner lists. We know the 9th item cannot be in the first inner list, since it only has 3 items. It also cannot be in the second inner list, since the first two lists combined only has 6 items. Instead, we can find the 9th item of the square list by looking for the 3rd item of the third inner list, which turns out to be 41.

To accomplish this search in O(√n) time, we must be able to determine the length of each inner list in O(1) time. In the worst case, we have to search through O(√n) items of the top-level list before we find the inner list that holds the i^th item. An additional O(√n) steps will allow us to find the desired item in that inner list, since the length of each inner list is also O(√n).

The main difficulty in maintaining a square list is that as we add items to and remove items from a square list, the length of the inner lists can change. This can happen in two ways. First, obviously, when we add items to or remove items from an inner list, the length of that inner list changes. Secondly, the length of an inner list relative to O(√n) can also change when we add or remove items elsewhere in the square list because doing so changes the value of n. For example, the 5th inner list in Figure 1 has 5 items. This happens to be exactly √25. If we removed all 10 items from the first 3 inner lists, that would leave us with only 15 items in the entire square list. Now the length 5th inner list is bigger than √15 even though the length of the 5th inner list remained at 5.

Square List Maintenance

Our goal is to make sure that the top-level list and all the inner lists have lengths bounded by O(√n). It is too expensive to require that our square list always has √n inner lists, each with √n items. Instead, we maintain the following two conditions:

Condition 1:

Every inner list has ≤ 2 √n items.

Condition 2:

There are no adjacent short inner lists, where short is defined as having ≤ √n/2 items.

Notice that neither condition says anything about the length of the top-level list. Instead, we claim that if Condition 2 holds, then the top-level list cannot have more than 4 √n items. Too see this, suppose the contrary. That is, suppose that the top-level list has more than 4 √n items. (Yes, this is the beginning of a proof by contradiction.) Then, there must be more than 2 √n inner lists that are not short (otherwise, two of the short inner lists would be adjacent). Thus, the total number of items in these non-short lists must exceed 2 √n × √n/2 = n. This is a contradiction because n is the number of items (by definition) and cannot exceed itself. Therefore, the number of inner lists (and thus the length of the top-level list) must be bounded by 4 √n.

These observations allow us to maintain the O(√n) bounds on the lengths of the top-level list and the inner lists using the following procedure:

Some notes on the Consolidate procedure:

• Our strategy for this project is to run Consolidate after every operation that adds an item to or removes an item from the square list. (This is a simplification. See Addendum for a longer explanation.)

• When two short lists are merged into one, the order of the items in the square list must not change. In Figure 2, the original order of the items in the short lists where 10, 21, 32, 14. In Figure 3, the order of the items in the merged list is the same.

• We need the data structure for the inner list to support a merge operation in constant time. A singly linked list with a tail pointer would work.

• In Figure 4, the inner list that is too long has an even number of items. If a long list has an odd number of items, then after the split, one list will have one more item than the other. This does not affect the asymptotic running time.

• When a long list is split, the order of the items must be preserved. (See Figure 4.)

• Without any splits, the total running time for the Consolidate procedure is O(√n), because we can merge short lists in constant time.

• The split step can be costly because it takes O(t) time to split an inner list in half, where t is the length of the inner list. We can show using amortized analysis that splits do not happen very often. The proof is not hard but is beyond the scope of this course. The amortized analysis gives an amortized running time of O(√n) for most of the list operations (except indexOf). The amortized analysis shows that any mix of m list operations (not including indexOf) will take a total running time of O(m√n). Thus, the amortized time for each of the m square list operations is O(√n). Although, it is tempting to think of the amortized running time as an "average" running time, this is not accurate because the amortized analysis does not depend on the sequence of operations being "nice" or "average" in any way. Even when an adversary chooses the nastiest sequence of operations which results in the maximum number of splits, the total running time for that sequence of m operations will still be bounded by O(m√n).

Fig. 2: A square list with adjacent short inner lists. Note that 2 < √22/2 ≈ 2.345.

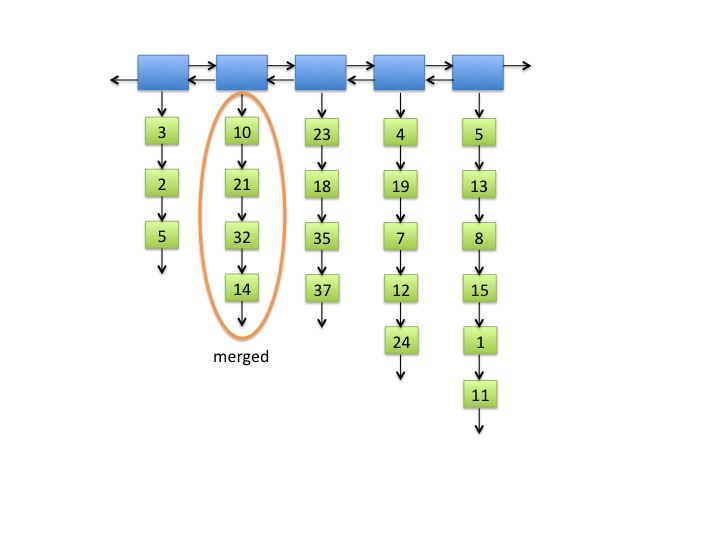
Fig. 3: Adjacent short lists merged.

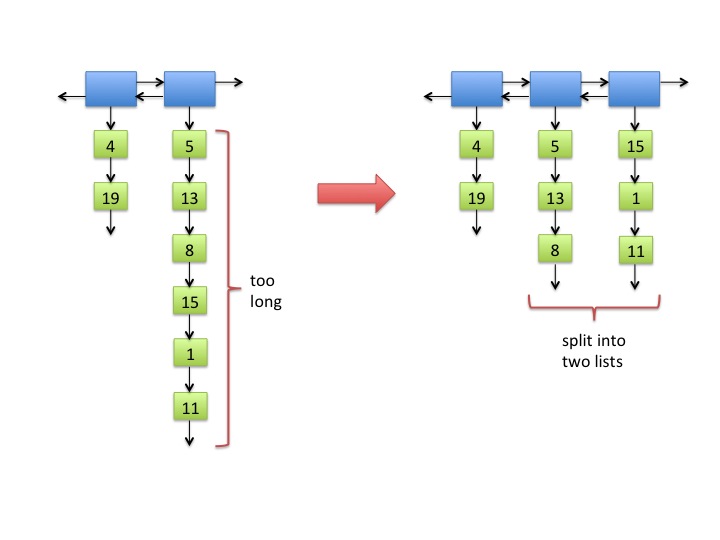
Fig. 4: A long inner list split into two lists. Note that 6 > 2 √8 ≈ 5.657.

Assignment

Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but exceed the required running times are considered wrong implementations and will receive substantial deductions during grading.

Your assignment is to implement a square list data structure that hold Java Integer values. The inner lists must be implemented as a singly-linked lists with dummy headers and tail pointers. This implementation should be your own work. In particular, you must not use any data structures from Java Collections API for the inner lists. For the top-level list, you must use the generic LinkedList class from the Java Collections API.

This assignment specifies the interface between the main program and your square list implementation, but you are free to design the data structure for the inner list as you please (subject to performance considerations listed below). Note that design is part of the grading criteria, so you do need to apply good design principles to your inner list data structure.

Your inner list class must have the following methods with the specified running times.

1. A method called merge() that merges two inner lists in constant time.

2. A method called size() that reports the length of an inner list in constant time.

3. A method called split() that divides an inner list into two lists of approximately equal size. (The lengths of the two lists should differ by at most 1.) This method should take O(t) time, where t is the length of the original inner list.

Your SquareList class must have the following methods with the specified signatures and running times.

1. A default constructor that initializes a SquareList properly. It should run in O(1) time.

2. A consolidate() method implemented as described above. This method should run in O(√n) time not counting splits. The splits should take time proportional to the length of the inner list that is split.

3. Two methods to insert at the beginning and at the end of a SquareList with the following signatures:

   public void addFirst (Integer data) 
   public void addLast (Integer data) 
   

   These methods should call consolidate() after insertion. They must run in constant time, not counting the time for consolidate().

4. A method to remove the item at the beginning of a SquareList with the following signature:

   public Integer removeFirst () 
   

   This method must return the Integer value that was at the beginning of the list or null if the list was empty. This method should call consolidate() after removal. The removeFirst() method should run in constant time, not counting the time for consolidate().

5. A method to add an item at a given position of a SquareList.

   public void add(int pos, Integer data) 
   

   Positions start at 0. Thus, add(0,5) should insert 5 at the beginning of the list. Also, if a square list originally held 1, 2, 3, 4, 5, then after add(2,99) the list should hold 1, 2, 99, 3, 4, 5. If pos is not valid, this method should do nothing. This method should call consolidate() after insertion. The add() method should take time O(√n) not counting the time for consolidate().

6. A method to remove an item from a given position of a SquareList and return its value.

   public Integer remove(int pos) 
   

   As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then after remove(3) the list should hold 1, 2, 3, 5. If pos is not valid, this method should return null. This method should call consolidate() after removal. The remove() method should take time O(√n) not counting the time for consolidate().

7. A method to return the value of an item at a given position of a SquareList.

   public Integer get(int pos) 
   

   As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then get(2) should return 3. If pos is not valid, this method should return null. The get() method should take time O(√n).

8. A method to change the value of an item at a given position of a SquareList.

   public void set(int pos, Integer data) 
   

   As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then after set(2,99) the list should hold 1, 2, 99, 4, 5. The set() method should take time O(√n).

9. A method that returns the number of items in a SquareList.

   public int size() 
   

   The size() method should run in constant time.

10. A method that returns the position of the first occurrence of a value in a SquareList.

    public int indexOf(Integer data) 
    

    If data does not appear in the list, then this method should return -1. As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then indexOf(5) should return 4. The indexOf() method should run in O(n) time.

11. A debugging method:

    public void dump() 
    

    The dump() method should print out the size of the SquareList and for each inner list, the size of the inner list, each item in the inner list and the item that the tail pointer references. The output should clearly indicate where an inner list begins and ends. The running time of dump() does not matter since it is used for debugging purposes only. However, you should implement dump() in the most reliable manner possible (i.e., avoid calls to methods which might themselves be buggy).

Finally, your square list class must be called SquareList and must be accessible from a main program in a different package. You can check that your code compiles correctly with this sample main program: Proj1Test.java. This test program must be placed in a separate directory named driver (since it belongs to the driver package). The output of Proj1Test.java should look something like this: Proj1Test.txt. The output may differ somewhat depending, for example, on how you split long lists with odd length. Your code must compile with Proj1Test.java without alteration.

Implementation Notes

• Start this project early. This is a two-week project, not a one-week project plus a one-week delay. You will most likely need all two weeks to finish.

• Apply the incremental programming methodology. Implement one or two methods and fully debug these methods before writing more code. Implement and fully debug your inner list data structure before you do anything for the SquareList class.

• Your data structure for the inner lists cannot be a doubly linked list.

• In a singly-linked list, a dummy header node is an extra node in the linked list that comes before the first node that contains data. When the list is empty, the list has just the header node and no other nodes. Having a header node simplifies coding for singly linked lists. For example, insertion at the beginning of the list does not require a special case.

• A tail pointer is not a tail node (which would not be very useful in a singly-linked list). A tail pointer is simply a reference to the last node in the linked list. When the list is empty, the tail pointer should reference the dummy header. Tail pointers make the merge operation fast, since we don't have to search the linked list to find the last node.

• Common errors while implementing singly linked lists with dummy headers and tail pointers:
  • Off-by-one errors: inserting or removing an item in the position one spot before or after
  • Forgetting to update the size of the list
  • Forgetting to update the tail pointer when the last item is inserted or removed

• You do not have to implement the full suite of list operations for the inner list data structure — just whatever is needed to support the SquareList operations.

• Be paranoid! Check that you are not merging a list with itself.

• Section 3.3 of the textbook has a good description of the generic LinkedList class and iterators.

• In the LinkedList class, the methods getFirst() and getLast() throw NoSuchElementException exceptions if the list is empty. Your code must catch these exceptions. (Otherwise it won't compile with Proj1Test.java.)

• The logic for the consolidate() method can be tricky. Think through this before coding.

• Do not use two iterators simultaneously on the LinkedList for the top-level list. You will need to use the remove() method when you delete empty inner lists and when you merge short lists. When you use one iterator to invoke the remove() method, it will invalidate the other iterator. When you use the next() method again, it will throw the exception: ConcurrentModificationException.

• Do write your own main program for testing. Proj1Test.java is a basic test that checks a few features and that your program will compile correctly. It is not a comprehensive test. Just because your program runs correctly with Proj1Test.java, it does not mean you will receive 100. It does not mean your program does not have bugs. Your program will be tested and graded against other main programs with bigger, meaner and nastier test cases. Just as an example, Proj1Test.java never checks if removeFirst() works correctly when the square list is empty, but you should.

• Do document your code.

What to Submit

Follow the course project submission procedures. You should copy over all of your Java source code with .java files in their own directories which are in turn under the src directory. You must also supply an Ant build file.

Make sure that your code is in the ~/cs341proj/proj1/ directory and not in a subdirectory of ~/cs341proj/proj1/. In particular, the following Unix commands should work. (Check this.)

cd ~/cs341proj/proj1
ant compile
ant run
ant clean

Discussion Topics

1. Suppose you start with an empty square list and keep inserting items in the front of the list. When does the first merge occur?

2. What is the smallest number of items you can have in a square list that has 11 inner lists?

3. Do we ever encounter long inner lists that have to be split (other than the first inner list) if we only allowed insertion and removal at the beginning of the list?

4. After you split an inner list, is it possible that the same inner list has to be split again after the very next square list operation? after two operations? when could the next split occur?

5. Can you ever encounter 3 short lists in a row during the Consolidate procedure? Does it matter? and should you write code whose correctness depends on the answer to these questions?

Addendum

Here are some ways we could improve the square list data structure. In particular, we can make addFirst(), removeFirst() and addLast() run in O(1) amortized time instead of O(√n) amortized time. Implementing these features would make the running time of set() and get() O(√n) amortized time instead of O(√n) worst case time.

However, do not submit code with these features as they will totally mess up the grading.

Early empty list deletion:

As soon as you notice that an inner list is empty, delete it. Don't wait for consolidate().

Don't make long lists:

In addFirst() and addLast(), start a new inner list if the length of the first or last inner list will exceed √n after insertion.

Early splits:

Whenever we perform an operation on an inner list that involves looking through the list (for example, a search, but not size()), split the list if the length is already greater than 1.5 √n. Since we are looking through the list already, we can do the split now instead of later.

Early merge:

Whenever we remove an item from an inner list, check to see if the inner list is now a short list. If the list is now short and an adjacent inner list is also short, we can merge those two now instead of waiting for consolidate(). This will only take an additional O(1) time.

Delayed Consolidation:

Don't consolidate after every operation that changes the length of the list. Wait for the number of inner lists to exceed 5 √n. It costs us O( √n) time just to look through the top-level list. We shouldn't do this for every addFirst() or addLast(), especially if we don't make long lists. Wait until enough short lists pile up and then merge them in one sweep.

Delayed Splits:

Long lists don't bother us unless we have to search through them. So, during consolidate, just ignore the long lists. The long lists will be split when we work with them if we implement early splits. This actually turns early splits into delayed splits, so we should adjust the threshold for early/delayed splits back to 2 √n.