Introduction To Digital Logic

The simpliest circuit we will deal with is:

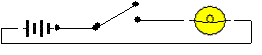
What we have is a power source (like a battery), a switch, and a lightbulb, like a simple flashlight. When the switch is open, the light is off. When the switch is closed, the light is on. This gives us open is a zero, and closed is a one. Now you should see this is a binary situation, and we can have a digital system.

AND Circuit

Now, if we add a second switch into the circuit and connect it to the first switch, the only way the light will be on is if both switches are closed.

We can show that in a truth table:

		Switch 2
		Open	Closed
Switch 1	Open	Off	Off
Switch 1	Closed	Off	On

OR Circuit

Now, if we add a second switch into the circuit and also connect it to the power source and the lightbulb, the only way the light will be off is if both switches are opened.

We can show that in a truth table:

		Switch 2
		Open	Closed
Switch 1	Open	Off	On
Switch 1	Closed	On	On

Now we can take those switches and package them as "gates", giving us an AND gate and a OR gate. We need one other basic gate, the NOT gate. It takes a one an makes it a zero or takes a zero and makes it a one.

On To The Basic Gates

AND	OR	NOT

Alternative Representations

NOT

A	B
0	1
1	0

AND

A · B

X^Y

A	B	F
0	0	0
0	1	0
1	0	0
1	1	1

A + B

A \/ B

A	B	F
0	0	0
0	1	1
1	0	1
1	1	1

Other Gates

That was too easy. What else can there be?

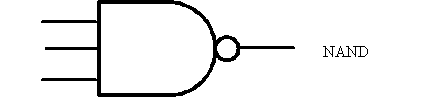
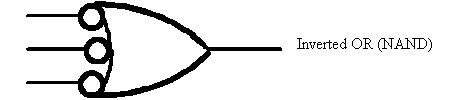
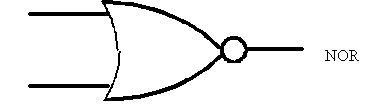
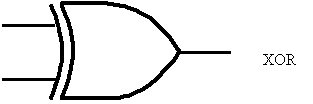
It gets hairy!

Contemporary Logic Design, 2^nd Edition, Randy Katz and Gaetano Borriello, 2005, Prentice Hall, Page 47