Final Exam Study Guide
You MUST present a picture ID
Exam Dates:
- Sections 0101 - 0104 (Frey) -- Tuesday May 20th, 10:30am - 12:30pm
- Sections 0201 - 0204 (Raouf) - Monday May 19th, 6:00 - 8:00pm
Use the list of questions below as a guide when studying for the final exam.
It is by no means a comprehensive list of all material that you are responsible for.
Like many other subjects, computer science is cumulative in nature.
We can't discuss each aspect of computer science in isolation.
Therefore, our final exam will also be cumulative. The vast majority (80% or more)
of the exam will be taken from material presented since the second exam.
The remaining 10-20% will be taken from other material we have covered this
semester.
I. Material Prior to Exam 2
General C++ topics
- basic class design and usage
- const vs non-const methods
- aggregation
- function overloading
- constructors, destructors, copy constructor, assignment operator
- file I/O using streams
- passing parameters by value, by reference, by reference to const
- returning objects by value, by reference, by reference to const
- strings, vectors
II. Recursion
Consider the following recursive mathematical function
f(n) = 1 if n = 0
f(n) = 4 if n = 1
f(n) = 2 * f(n - 1) - f( n - 2) for n > 1
- Write the syntactically correct C++ implementation of this function.
- What is/are the base case(s)?
- Classify this function as direct, indirect, linear and/or tree recursion.
- What is the value of f(5)?
- Digram the recursive calls which occur when calculating f(5).
- What is/are the precondition(s) for this function?
Consider the following code. Recall that adding strings ( operator+ )
results in string concatenation.
const string a = "0123456789ABCDEF";
string mystery(int n)
{
if (n <= 0)
return ("");
else if (n <= 15)
return (a[ n ]);
else
return mystery( n / 16) + (a[ n % 16 ]);
}
- What is the output of cout << mystery( 34 ) << endl; ?
- What is the output of cout << mystery( 255 ) << endl; ?
- In general, what does mystery do?
Consider the following code
#include <iostream>
using namespace std;
void mystery (int n)
{
if (n > 1)
{
cout << n << endl;
if (n % 2 != 0)
mystery( 3 * n + 1 );
else
mystery( n / 2 );
}
}
int main()
{
mystery ( 3 );
return 0;
}
- What is the output from the code?
- Under what condition(s) will this code cause infinite recursion?
(Note: you can cut/paste this code into a .C file and compile/link/run
it to verify your answer).
- What is the difference in the behavior of these two
recursive functions? Why does this difference occur?
|
void write (int n)
{
if (n >= 1)
{
cout << n << end;
write (n - 1 );
}
}
|
void write (int n)
{
if (n >= 1)
{
write (n - 1 );
cout << n << end;
}
}
|
- List three advantages of iteration over recursion.
- List three advantages of recursion over iteration.
- Use recursion to implement the traversals of a binary tree.
III. Sorting and Searching
- Given a non-empty unsorted array with 17 elements
- What is the minumum number of comparisons performed by
a linear search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the minimum?
- What is the maximum number of comparisons performed by
a linear search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the maximum?
- What is the average number of comparisons performed by
a linear search when attempting to find a value in the array?
- Generalize your answers for an array of N elements.
- Given a non-empty sorted array of 17 elements
- What is the minumum number of comparisons performed by
a linear search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the minimum?
- What is the maximum number of comparisons performed by
a linear search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the maximum?
- What is the average number of comparisons performed by
a linear search when attempting to find a value in the array?
- What is the minumum number of comparisons performed by
a binary search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the minimum?
- What is the maximum number of comparisons performed by
a binary search when attempting to find a value in the array?
Under what conditions would the number of comparisions be the maximum?
- What is the average number of comparisons performed by
a binary search when attempting to find a value in the array?
- Generalize your answers for an array of N elements.
- Given the sorted array
a[ ] = { 1, 3, 5, 7, 9, 12, 18, 22, 23, 30, 35, 39, 41, 44, 46, 50, 51}
List the values which will be checked when performing
a binary search for the value 47.
- Given the array a[] = { 12, 87, 22, 6, 19, 44, 92, 21},
diagram the execution of mergesort (merge) to sort the array.
- Given the array a[] = { 12, 87, 22, 6, 19, 44, 92, 21},
diagram the execution of quicksort (partition) to sort the array.
- The MergeSort code on the web sorted an array of integers,
but the algorithm for MergeSort is data-independent. Rewrite MergeSort()
as a function template.
- What are the precondition(s) for mergesort?
- What are the precondition(s) for quicksort?
- List one difference between quicksort and mergesort.
- List one similarity between quicksort and mergesort.
IV. Trees
For these questions, the C++ class definition of
a General Tree, BinaryTree, BinarySearchTree
(BST) and TreeNode will be provided if/when necessary
- Given a general tree's first-child, next sibling representation, draw the tree.
- Given a general tree, draw its first-child, next sibling representation.
- For any tree T, define
- path in T
- length of a path in T
- depth of a node in T
- height of a node in T
- the depth of T
- the height of T
- Define full binary tree, perfect binary tree
- Define internal node and external node in a rooted tree.
- Write the syntactically correct recursive C++ code for in-order,
pre-order or post-order traversal for a binary tree.
- Given the array a[ ] = { 50, 30, 20, 66, 42, 77, 70, 2 }
Draw the tree that results from inserting these values into an
initially empty BST.
- Given the BST
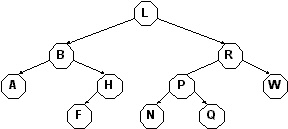
- What is the output from an in-order traversal of the BST?
- What is the output from an pre-order traversal of the BST?
- What is the output from an post-order traversal of the BST?
- What is the output from a breadth-first traversal of the BST?
- Draw the BST using first-child, next-sibiling representation
- Add the value 'V' to the tree
- Write a syntactically correct function which might be part of a BST class,
or use a BST as a parameter. For example
- FindMin( ) that finds and returns the minimum value in a BST
Write both the iterative and recusive versions.
- PrintTree( ) that prints the data from each node in the BST in post-order.
- BST destructor.
- Insert the values {2, 4, 5, 7, 12, 15, 19} into an initially empty BST.
What is the shape of the tree? Why is this so?
- Explain why the BST destructor must use a post-order traversal of the tree.
- Explain why an in-order traversal of a BST always results
in the data being printed in sorted order.
- Write the code for a Breadth-First Search of a binary tree.
- Write the code for a Depth-First Search of a binary tree.
