Due at the start of class on Tuesday February 21
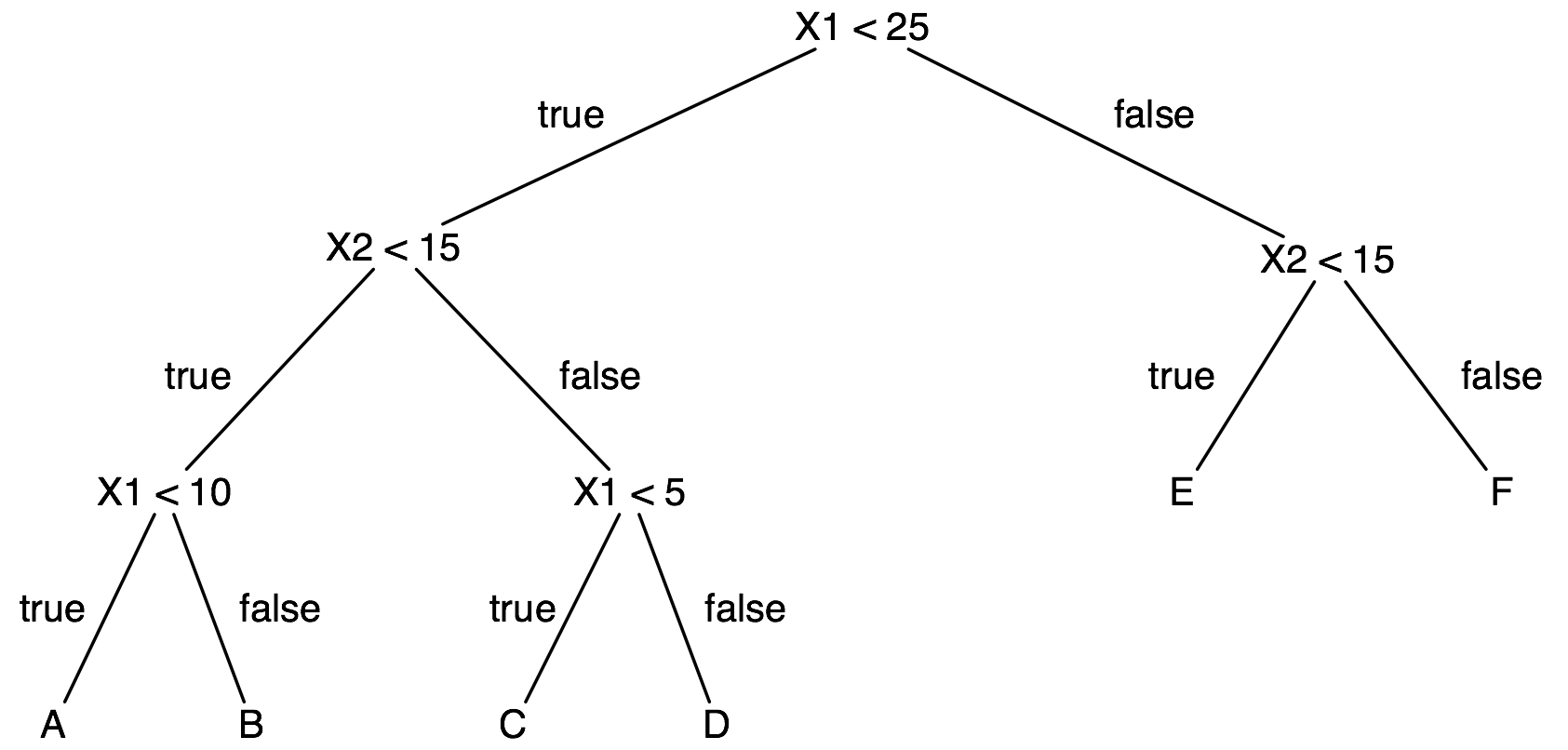
(1) Consider the following decision tree:

(A; 10 pts) (478 and 678 students) Draw the decision boundaries defined by this tree. Each leaf is labeled with a letter. Write this letter in the corresponding region of instance space.
(B; 10 pts) (478 and 678 students) Give another decision tree that is syntactically different but defines the same decision boundaries. Your answer must be in the form of a decision tree. This demonstrates that the space of decision trees is syntactically redundant.
(C) (678 students only; 10 pts) Does the fact that the hypothesis space of decision trees has this kind of redundancy have any implications for learning decision trees? In particular, comment briefly on whether this redudancy makes it more difficult to find accurate trees (as opposed the inaccurate trees) and whether it makes decision tree learning more computationally expensive.
(2) Suppose you want to train a perceptron on the following dataset:
| X1 | X2 | Y |
| 2 | 6 | -1 |
| 1 | 3 | 1 |
| 3 | 9 | 1 |
(A) (478 and 678 students; 15 pts) Give a brief intuitive explanation for why the perceptron cannot learn this task. Then give a proof using inequalities expressed in terms of the weights W1, W2, and b. Recall that y*a must be > 0 for the perceptron to classify an instance correctly. You should show that this condition cannot be satisfied simultaneously for all 3 instances above for any W1, W2, and b.
(B) (478 and 678 students; 10 pts) Imagine that we modify the perceptron algorithm given in the book so that it always updates the weights. That is, we don't first check to see if y*a ≤ 0 before doing a weight update. Is the resulting algorithm still correct? That is, will it still be able to classify linearly separable data perfectly? Why or why not? Will the weights eventually converge and cease to change? Why or why not? If they don't converge, characterize what happens to them as the number of iterations grows large.
(3) Geometry
(A) (478 and 678 students; 10pts) Draw a dataset (collection of points) in 2 dimensions. Pick two points as initial centroids for 2-means clustering and show the clusters that would result. Make a copy of the same data and show two different points that result in a different final clustering. Be sure to show that final clustering as well.
(B) (478 and 678 students; 10 pts) Draw a dataset (collections of points and their class labels, either + or -) in 2 dimensions such that if you iterate over all points p in the dataset, remove p, and ask what its label is using the 1-NN classifier you would get 0% accuracy. Describe briefly how common you think this pathological behavior is in real world datasets.