CMSC671, Homework2 Background and Design Guidance
Sudoku
Sudoku is a game that consists of an NxN grid or array.
The cells in this array are arranged into blocks. The standard game
consists of 9 (3x3) blocks of 9 (3x3) cells each. The simple games we'll
solve in this assignment consist of 4 (2x2) blocks of 4 (2x2) cells each.
In general, if there are XBLOCKS x YBLOCKS blocks, then each
block will contain YBLOCKS x XBLOCKS cells. Here are some
examples of possible Sudoku grids, with the blocks delineated by heavier lines:
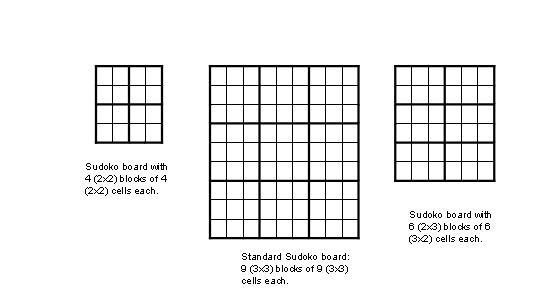
Each cell will contain a number from 1 to XBLOCKS*YBLOCKS.
In a solved Sudoku game, every row, column, and block must contain exactly
one of each number. That is, every cell must be filled with a
number, and there can be no duplicated numbers in any row, column, or block.
Here are a couple of definitions that you'll need:
- A game state is a board where each cell is either empty
or contains a number from 1 to XBLOCKS * YBLOCKS.
- A legal game state is a game state that satisfies the
Sudoku constraints: i.e., one in which there are no duplicated numbers in any
row, column, or block.
- A solution state is a game state in which no cell is
empty.
- A legal solution state is a solution state that is
also a legal game state.
For a given initial game state, there will be zero or more
associated goal states. Each of these goal states satisfies the
following conditions: (a) the goal state must be a legal solution state, and (b)
any cell that is non-empty in the initial game state must contain that same
value in the goal state.
Infrastructure
You should download the file sudoku-basics.lisp.
Read the documentation in the file thoroughly to be sure that you
understand the code. The file includes a definition for the game CLOS
class; a function to create a new game instance; and a number of utility,
debugging/logging, and I/O functions.
A couple of notes on the Lisp code in this file:
- Some of the functions are implemented using Lisp's macro
capability. This is an efficient way to do in-place expansion, giving a
shorthand representation for frequently used code fragments without the
overhead of a function call. If you decide to use macros in your own code, be
sure you read up on them first, since getting the right things to
evaluate at the right time with the backquote-comma (` ,) syntax can
be tricky.
- I've used an array to represent the game board. The main
functions you need to know for manipulating arrays are make-array,
array-dimensions, and aref, which dereferences an
array location.
- For this assignment, you won't need to do much I/O. However,
you might want to take a look at this function and the debugging
functions to learn how some of the basic I/O functions work (open, close,
with-open-file, print-object, read,
and read-line). You may want to write some output to a
file in order to record the data that I've requested.
Notes on Coding in Lisp
Because Lisp is an interpreted language, it's very easy to test code
fragments. I highly recommend testing every function independently
before moving on to the next one (as opposed to writing all of your code,
loading it all in, and starting to debug the whole thing at once). You can
debug bottom-up by testing low-level functions thoroughly before testing
the higher-level functions that call them. You can also debug top-down
by writing "stub" functions at lower levels that serve as place holders
for the low-level functions, allowing you to test the higher-level
functions and the overall structure of the code before adding the low-level
functions.
The variable *solved* contains the simplest possible
case -- a board that has already been solved -- so you may want to use this
for your initial debugging. From there, you can progress to *easy-test*,
which contains a board with only one empty slot.
Implementation Suggestions
This approach is one suggested way to develop your
implementation. You should read this entire section before you get started These
notes are just an overview; you'll still need to figure out how to design
the pieces and "glue" them together to have a working system.
The code I have provided contains some helper macros called BLOCK-GROUPS, ROW-GROUPS,
and COLUMN-GROUPS. Given a game board, these macros will
each generate a list of lists. Each of these lists contains the
numbers in one of the blocks, rows, or columns on the board (which must be
consistent in size with the current definitions of XBLOCKS and YBLOCKS,
as defined earlier (and defined with defvar in sudoku-basics.lisp).
You should try these out on the sample boards I have given you.
Once you understand these macros, you can use them to write a
"constraint checking" function, LEGALP, that tests to see whether the
board is a legal board. Now it should be easy to write the GOALP function,
which takes one argument (a game instance) and returns T if the
specified game board is in the goal state. Test this function on the test games
provided.
Note that you will also need a way to determine how many legal choices there
are for each cell, in order to write the best-first search heuristic, so you
might want to think about that when designing the LEGALP function.
The next thing to think about is designing the operators (i.e.,
writing the EXPAND function to generate the successor states).
At any given point in the search, you can fill in a single square with a
single value. I'm leaving the design of this up to you, since there are a
number of perfectly reasonable ways to do this. One important
thing to think about is when you want to test for the legality of a state. For
example, you could simply loop across the game board, trying to apply each
of the operators (i.e., each of the XBLOCKS * YBLOCKS values) to
each of the empty board locations, testing the resulting game board using the
LEGALP function, and collecting a list of resulting
states.
Alternatively, you could use some more "intelligent" approach to
pre-compute the possible legal values, and reduce the amount of work that EXPAND
has to do. For this assignment, as long as your code is
working and reasonably efficient, it doesn't matter to me how you implement this
function.
At this point, you should be ready to write the BASIC-SEARCH
function as given in Russell & Norvig's Figure 3.9. Note that
the queueing function is sent into this function -- the best way to do
this is to send in the function binding, e.g., #'q-bfs,
and use (funcall q-fn ARG ...) to invoke the queuing
function.
Detecting repeated states is important in this domain, and you'll
need to be able to run your code with and without checking for
repeated states in order to gather the data I have asked for. You may
want to have this function maintain a CLOSED list (list of nodes
that have been expanded) as well as the usual OPEN list. You'll
probably want a separate function to detect repeated states and remove
them from the list of new nodes, or you could do this check in the EXPAND
function. (Note that the code has ARRAY-EQUAL,
which can be used to test whether two game boards are the same.)
To make repeated state checking optional, you can add an
optional argument repeated-state-p to your search functions, which
defaults to NIL but can be set to T to turn on repeated state
checking.
You should also keep track of the cumulative number of generated and
expanded nodes, since you'll need to report those in your final
results.
This function should return a list of four things: either the
symbol
'SUCCESS or 'FAIL, the goal node found, the number
of created nodes, and the number of expanded nodes. You can then use
these results to print a summary of the search.
Write Q-BFS (the breadth-first function to be called by BASIC-SEARCH)
and BFS (a wrapper that invokes BASIC-SEARCH with Q-BFS).
Write Q-DFS (the depth-first queuing function to be
called by BASIC-SEARCH) and DFS (a wrapper that invokes BASIC-SEARCH
with Q-DFS). These functions should just be a line or
two each.
Finally, if you want to make use of the aima (textbook) code repository, you should notice that they use DEFSTRUCT for defining the problems. The code I have provided uses DEFCLASS for the same purpose.
Both have similar functionality in Lisp, except that defstruct (automatically) defines a constructor function that is used to create instances of the structure created by defstruct. The default name is make-structure-name.
The general search function and the specific search algorithms in the aima code follow the structure you have been asked to implement for this homework (they reflect the algorithms in the book). You might want to take a look at the general-search function for help. If you decide to use code from the repository you will have to represent the problem (sudoku) appropriately and make sure you have the same test cases (*test1* through *test9*). 