CMSC 671

Artificial Intelligence -- Fall 2010

Mini-Project
out 9/15/10; due 10/6/10


In this assignment, we'll explore the search space of the game Sudoku. I've provided some Lisp infrastructure (data structures, basic variables, and some helpful macros and functions). I've also given you some moderately structured guidance on how to design and implement a solution. You do not have to follow my guidance, or use my code, as long as you provide working Lisp code with the specified functionality.

You may modify the code I've provided, but please maintain the provided code and your new code in separate files, and document any changes that you make to the provided code.

VERY IMPORTANT:  You need to pace yourself with this assignment. You have three weeks, rather than the usual two weeks for a homework assignment, in order to give you some flexibility in managing your time and designing your software. I strongly suggest that you use this time wisely.  For example, you may want to allocate the first week to implementing the basic form of the search algorithnm, which should be able to apply BFS and DFS to at least *test1* and ideally *test2*, and should be able to do repeated state checking.  Use the second week to finish your implementation (record the appropriate data, implement queue/time limits, and implement queue ordering), testing on the larger problem. Use the third week to analyze your data and write your summary report. Be sure you do leave enough time to write the report, since it is worth 25% of the assignment.

SHARING CODE:  Student are welcome to share "helper" functions such as I/O, experiment wrappers, and data collection functions with each other.  In fact, I encourage this kind of collaboration.  However, you may not share any code that manipulates the problems themselves, the search space, the states, or the solutions. As the course and honesty policy states, you may not show your code to any other student. You may not incorporate code from any other source (beyond the helper functions I've provided), even with documentation -- you should write your own solution to this -- -- assignment.  When in doubt, please ask first.

1. Implementation (75 points)

Implement a generic uninformed search function, along the lines of the algorithm from the course slides. Write a wrapper function that invoke this generic search function to perform breadth-first, depth-first, and best-first search in the Sudoku search space. Your best-first search should sort the queue of nodes using a "maximally constrained" heuristic.  That is, actions that fill empty cells where there is only one legal choice remaining should be tried first; next, try actions that fill empty cells for which there are two legal choices; and so on.

 Include mechanisms to limit the length of the queue and/or computation time and to test for repeated states. (You will probably need to do a bit of experimentation to find reasonable values for the queue and time limits.  Don't make them too low or you won't be able to solve many of the problems.)  Test your code thoroughly, and make sure it's sufficiently well documented for us to read it and understand what it's doing.

Very important: Some of the search spaces will grow quite large, and I don't necessarily expect your implementation to be able to solve all of the problems..

2. Results and Discussion (25 points)

Run breadth-first, depth-first, and best-first search, with and without repeated-state checking, on the test cases *test1* through *test9* (given in the sudoku-basics.lisp file).  (In total, you should have 3 searches * 2 options * 9 test cases = 54 runs.)  Submit a well-organized report that summarizes your findings, and that discusses the questions below.  (Note that the tests have different array sizes.  The only function for which this should matter is the BLOCK-GROUPS function, which I've provided.  However, you'll need to reset XBLOCKS and YBLOCKS appropriately before invoking your solver.)

At a minimum, you should show, for each of the 54 runs, the number of nodes generated, number of nodes expanded, and CPU time consumed. You may present this data in a graph, chart, or table -- whichever you think will be most understandable and most effectively support your conclusions. (You will probably want to write a "wrapper" function to run all of the experiments and gather the statistics together.)

Your report should answer the following questions (though it does not need to be organized in this order, and you are certainly welcome to include additional observations, experiments, or ideas):
  1. Did the algorithms find a solution in all cases?  If not, why not?
  2. How did the various measures of run time (nodes generated/expanded and CPU time) compare for breadth-first search and depth-first search?
  3. How did checking repeated states affect the various measures of run time?  Was this effect different for the different algorithms (BFS vs. DFS)?  Why or why not?
  4. In this domain, what does it mean for a search to be optimal?  What does it mean for a search to be efficient?
  5. How did you find a reasonable queue limit and/or time limit?  How would the algorithms behave if you increased or removed these limits?
  6. How did queue ordering affect the various measures of run time?  Was this effect different for the different algorithms?  Why or why not?
  7. I didn't mention the possibility of using a depth limit, or iterative deepening search.  Would either of these be helpful?  Why or why not?


Background and Design Guidance

Sudoku

Sudoku is a game that consists of an NxN grid or array.  The cells in this array are arranged into blocks.  The standard game consists of 9 (3x3) blocks of 9 (3x3) cells each.  The simple games we'll solve in this assignment consist of 4 (2x2) blocks of 4 (2x2) cells each.  In general, if there are XBLOCKS x YBLOCKS blocks, then each block will contain YBLOCKS x XBLOCKS cells.  Here are some examples of possible Sudoku grids, with the blocks delineated by heavier lines:
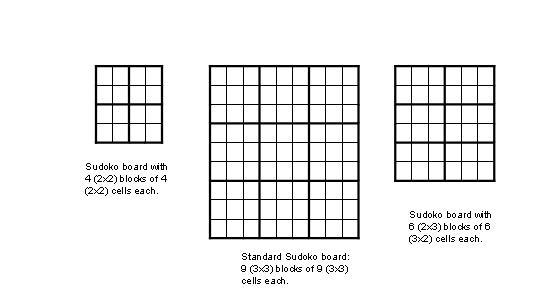
<sudoko grids>

Each cell will contain a number from 1 to XBLOCKS*YBLOCKS.  In a solved Sudoku game, every row, column, and block must contain exactly one of each number.  That is, every cell must be filled with a number, and there can be no duplicated numbers in any row, column, or block.

Here are a couple of definitions that you'll need:
For a given initial game state, there will be zero or more associated goal states.  Each of these goal states satisfies the following conditions: (a) the goal state must be a legal solution state, and (b) any cell that is non-empty in the initial game state must contain that same value in the goal state.

Infrastructure

You should download the file sudoku-basics.lisp. Read the documentation in the file thoroughly to be sure that you understand the code. The file includes a definition for the game CLOS class; a function to create a new game instance; and a number of utility, debugging/logging, and I/O functions.

A couple of notes on the Lisp code in this file:

Notes on Coding in Lisp

Because Lisp is an interpreted language, it's very easy to test code fragments. I highly recommend testing every function independently before moving on to the next one (as opposed to writing all of your code, loading it all in, and starting to debug the whole thing at once). You can debug bottom-up by testing low-level functions thoroughly before testing the higher-level functions that call them. You can also debug top-down by writing "stub" functions at lower levels that serve as place holders for the low-level functions, allowing you to test the higher-level functions and the overall structure of the code before adding the low-level functions.  The variable *solved* contains the simplest possible case -- a board that has already been solved -- so you may want to use this for your initial debugging.  From there, you can progress to *easy-test*, which contains a board with only one empty slot.

The tools I primarily use for debugging are tracing, format statements in the text, and the step function. There is also some built-in functionality in Lisp for inspecting the stack and data objects, but I personally find that the interface for doing this in CLISP is not very easy to use.

Implementation Suggestions

This approach is one suggested way to develop your implementation. You should read this entire section before you get started These notes are just an overview; you'll still need to figure out how to design the pieces and "glue" them together to have a working system. 

I've written some helper macros called BLOCK-GROUPS, ROW-GROUPS, and COLUMN-GROUPS.  Given a game board, these macros will each generate a list of lists.  Each of these lists contains the numbers in one of the blocks, rows, or columns on the board (which must be consistent in size with the current definitions of XBLOCKS and YBLOCKS, as defined earlier (and defined with defvar in sudoku-basics.lisp).  You should try these out on the sample boards I've given you.

Once you  understand these macros, you can use them to write a "constraint checking" function, LEGALP, that tests to see whether the board is a legal board.Now it should be easy to write the GOALP function, which takes one argument (a game instance) and returns T if the specified game board is in the goal state. Test this function on the test games provided. (Hint: the built-in Lisp function every may come in handy.)  Note that you will also need a way to determine how many legal choices there are for each cell, in order to write the best-first search heuristic, so you might want to think about that when designing the LEGALP function.

The next thing to think about is designing the operators (i.e., writing the EXPAND function to generate the successor states).  At any given point in the search, you can fill in a single square with a single value.  I'm leaving the design of this up to you, since there are a number of perfectly reasonable ways to do this.  One important thing to think about is when you want to test for the legality of a state. For example, you could simply loop across the game board, trying to apply each of the operators (i.e., each of the XBLOCKS * YBLOCKS values) to each of the empty board locations, testing the resulting game board using the LEGALP function, and collecting a list of resulting states.  Alternatively, you could use some more "intelligent" approach to pre-compute the possible legal values, and reduce the amount of work that EXPAND has to do.  For this assignment, as long as your code is working and reasonably efficient, it doesn't matter to me how you implement this function.  For the next assignment, we'll be exploring some different approaches for generating the alternatives more efficiently and intelligently.

At this point, you should be ready to write the BASIC-SEARCH function as given in Russell & Norvig's Figure 3.9. Note that the queueing function is sent into this function -- the best way to do this is to send in the function binding, e.g., #'q-bfs, and use (funcall q-fn ARG ...) to invoke the queuing function.

Detecting repeated states is important in this domain, and you'll need to be able to run your code with and without checking for repeated states in order to gather the data I've asked for.  You may want to have this function maintain a CLOSED list (list of nodes that have been expanded) as well as the usual OPEN list. You'll probably want a separate function to detect repeated states and remove them from the list of new nodes, or you could do this check in the EXPAND function. (Note that I've given you ARRAY-EQUAL, which can be used to test whether two game boards are the same.)  To make repeated state checking optional, you can add an optional argument repeated-state-p to your search functions, which defaults to NIL but can be set to T to turn on repeated state checking.

You should also keep track of the cumulative number of generated and expanded nodes, since you'll need to report those in your final results. This function should return a list of four things: either the symbol 'SUCCESS or 'FAIL, the goal node found, the number of created nodes, and the number of expanded nodes. You can then use these results to print a summary of the search, including the path back to the node (assuming you've linked all of your parent nodes correctly!)

Write Q-BFS (the breadth-first function to be called by BASIC-SEARCH) and BFS (a wrapper that invokes BASIC-SEARCH with Q-BFS). Write Q-DFS (the depth-first queuing function to be called by BASIC-SEARCH) and DFS (a wrapper that invokes BASIC-SEARCH with Q-DFS). These functions should just be a line or two each.

You're done! :-) (modulo queue limits, queue ordering, testing, gathering results, debugging, getting rid of the infinite loops...)