CMSC 671
Artificial Intelligence -- Fall 2010
HOMEWORK TWO
out 9/22/10 due 10/13/10
As always, this assignment must be turned in as a hardcopy.
You may either typeset your solution or handwrite them neatly.
PART I. Constraint Satisfaction (50 pts.)
In this question, you will be solving a map-coloring problem. In
this
domain, each of the regions on a map must be colored either black, gray,
or
red. The regions
must be colored in such a way that no adjacent regions are the same
color.
Two regions are considered to be adjacent if they touch along an
edge.
(Two regions that touch only at a corner are not adjacent.) Here
is
the map that you'll be using for all of the questions in this section:
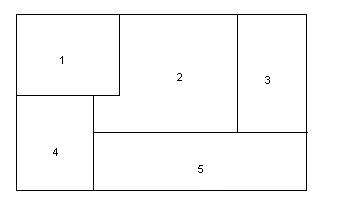
1. Backtracking search (15 pts)
Suppose you decide to use simple backtracking search to find a solution
to
this constraint satisfaction problem. The variable ordering
heuristic
you use is simply to instantiate the variables in numbered order.
The
value ordering heuristic is to consider the values in the order black,
gray,
red. You can use any reasonable shorthand to indicate the
instantiations
(e.g., "1=B" can mean region 1 is instantiated to the color black).
(a) Show the complete search tree, circling the solution node, if
one
is found.
(b) Show the final coloring, if one is found, on the map above or on
a copy of the map.
(c) How many variable instantiations (search steps) are tried by
this
search method?
2. Forward checking (20 pts)
Now suppose we use forward checking to eliminate illegal values from
the
domains of uninstantiated variables. (Recall that in forward
checking,
only the constraints immediately connected to instantiated variables are
checked.) Furthermore, suppose we use a variable ordering
heuristic
that chooses the variable with the fewest legal instantiations remaining
to instantiate next. If more than one such variable exists, the
one
earlier in the numbered order is selected. The same value ordering
heuristic is used as in backtracking search (i.e., consider first black,
then gray, then red).
(a) Show the complete search tree for forward checking search.
At
each node, show the remaining legal values for the uninstantiated
variables.
For example, at the first node below the root, only region 1 will be
colored,
so you should indicate the legal values for variables 2, 3, 4, and
5.
Continue until your search finds a solution or fails.
(b) Show the final coloring, if one is found, on a copy of the map
above.
(c) How many variable instantiations are tried by this search
method?
3. Solution spaces (15 pts)
(a) How large is the search space for this problem? That
is,
how many different colorings, legal or illegal, are there for the blank
map shown above?
(b) For this map, how many different solutions (legal
colorings)
are there?
PART II. Game Playing (50 pts)
Recall the game of Nim that we played in class. Initially, there are k
piles, each containing nk sticks. Two
players
alternate turns, and at each turn the current player removes any
positive
number of sticks from one of the piles. At least one stick
must
be removed during a turn. The last player to remove a stick loses.
We
will represent a state in this game as a k+1-tuple:
[s1 ... sk p],
where si is in the interval [0,nk], and represents
the
number of sticks remaining in pile i; and p is either A or
B,
representing which player's move is next.
For those problem, you will be considering Nim211, a variation of Nim
with
three piles: one containing two sticks and the others each containing
one
stick. Player A goes first, so the initial state is [211A].
1. Game Tree (15 points)
Draw the complete game tree for Nim32. The left-to-right
order
of actions taken should always be: remove 1 stick from pile 1,
remove
2 sticks from pile 1, remove 1 stick from pile 2, remove 1 stick
from
pile 3. (Obviously you should only have branches for actions that
are
legal in a particular state.) We will ignore the issue of repeated
states for this problem, so it's OK if a state appears in more than one
place
in your tree.
2. Minimax and Alpha-Beta (15 points)
(a) Mark the terminal nodes in the game tree you drew for
Question
II.1 with their utility values, using +1 to indicate a win for A (MAX),
and
-1 to indicate a win for B
(MIN).
(b) Annotate each of the nodes in the tree with its backed-up
minimax
value.
(c) Circle the nodes that would be pruned by alpha-beta pruning
using
depth-first (left-to-right) search. (You should assume that the alpha
values
are initialized to -1, rather than -infinity, and that the beta values
are
initialized to +1, rather than +infinity.)
3. Expectiminimax (20 pts)
Now suppose that each player only gets to choose which pile to draw
from,
but not how many sticks to remove. Instead, the number of sticks
removed
is a random integer in the interval [0, sk]. For
example,
if the player chooses pile 2 and there are two sticks remaining in pile
2,
then with probability 1/3, no sticks are removed; with probability 1/3,
one
stick is removed; and with probabiity 1/3, two sticks are removed.
Draw the 2-ply expectiminimax tree (i.e., one move for each player).
Use
the expectiminimax tree to back up the expected, max, and min values at
each
node. For the static evaluation function, use the (backed-up)
utility
values from the game tree you generated in II.2.
