Our agent is hungry and unhappy, and wants to be happy and not hungry (goal state). Our agent starts out rich, but only has limited options, some of which will consume a substantial part of its wealth.
| have(car) | The agent has a car | |
| distance(x,y,d) | The distance from x to y is d; distance is assumed to be reflexive; i.e., distance(x,y,d) <=> distance(y,x,d) | |
| temp(x,t) | The temperature at location x is t | |
| in(r,x) | Restaurant r is in city x | |
| beach(x) | There is a beach in location x | |
| fastfood(r) | r is a fast-food restaurant | |
| swanky(r) | r is a swanky restaurant |
| at(x,s) | The agent is at x in situation s | |
| happy(s) | The agent is happy in situation s | |
| hungry(s) | The agent is hungry in situation s | |
| rich(s) | The agent is rich in situation s |
| Balt | Baltimore | |
| Berm | Bermuda | |
| OC | Ocean City | |
| McDs | McDonald's | |
| BK | Burger King | |
| CTC | Chez Tres Cher | |
| MC | Molto Caro |
(a) (10 pts.) Describe only the Happy predicate using the situation calculus. You should have one or more possibility axioms (one for each relevant action) and one or more successor-state axioms (one for each relevant action). These axioms should characterize how the state of the Happy predicate changes as a result of the actions in the domain, in terms of the domain predicates listed above.
(b) (10 pts.) Describe the actions in this domain as STRIPS operators. Be sure to include all preconditions, add lists, and delete lists.
(c) (5 pts.) Show two different legal plans (sequences of actions) for achieving the goal described above from the given initial state.
(d) (5 pts.) How many legal plans are there for this goal? Explain your
answer. Does the answer change depending on whether or not repeated
states are allowed?
(a) (10 pts.) Suppose that the agent starts building a partial-order plan to achieve the goal in the domain from problem #1. The agent decides to drive to Ocean City and eat at Burger King. Draw the partial-order plan at this point in the planning process. You do not need to show the dependencies associated with static predicates. Show all dependencies (ordering links and causal links) associated with dynamic predicates. Ordering links should be drawn as a thin, single arrow; causal links, as a double or thick arrow.
(b) (10 pts.) Now suppose that the agent decides to satisfy its Happiness goal using the Sunbathe action. Insert this action into the plan, showing all dependencies.
(c) (10 pts.) Will the plan produced in part (b) succeed? If so, complete the partial plan, resolving any
threats that arise. If not, complete the partial plan to the point where
planning fails, and explain the source of the failure.
The diagram below shows a gridworld domain in which the agent starts at the upper left location. The upper and lower rows are both "one-way streets," since only the actions shown by arrows are available.
Actions that attempt to move the agent
into a wall (the outer borders, or the thick black wall
between all but the leftmost cell of the top and bottom
rows) leave the agent in the same state it was in with
probability 1, and have reward -2.
If the agent tries to move to the right from the upper right
or lower right locations, with probability 1,
it is teleported to the far left end
of the corresponding row, with reward as marked.
All other actions have
the expected effect (move up, down, left, or right)
with probability .9, and leave the agent in the same state it was
in with probability .1. These actions all have utility -1,
except for the transitions that are marked. (Note that the
marked transitions only give the indicated reward if the action
succeeds in moving the agent in that direction.)
(a) MDP (10 pts) Give the MDP for this domain
only for the state transitions starting from each of
the states in the top row, by filling in a
state-action-state
transition table (showing only the state transitions
with non-zero probability). You should refer to each state
by its row and column index, so the upper left state is [1,1]
and the lower right state is [2,4].
To get you started, here are the first few lines of the table:
| State s | Action a | New state s' | p(s'|s,a) | r(s,a,s') |
| [1,1] | Up | [1,1] | 1.0 | -2 |
| [1,1] | Right | [1,1] | 0.1 | -1 |
| [1,1] | Right | [1,2] | 0.9 | +20 |
(b) Value function (15 pts)
Suppose the agent follows a randomized policy π (where each
available action in any given state has equal probability)
and uses a discount factor of γ=.85.
Given the partial value function (Vπ; Uπ in
Russell & Norvig's terminology) shown below,
fill in the missing Vπ values. Show and explain your work.
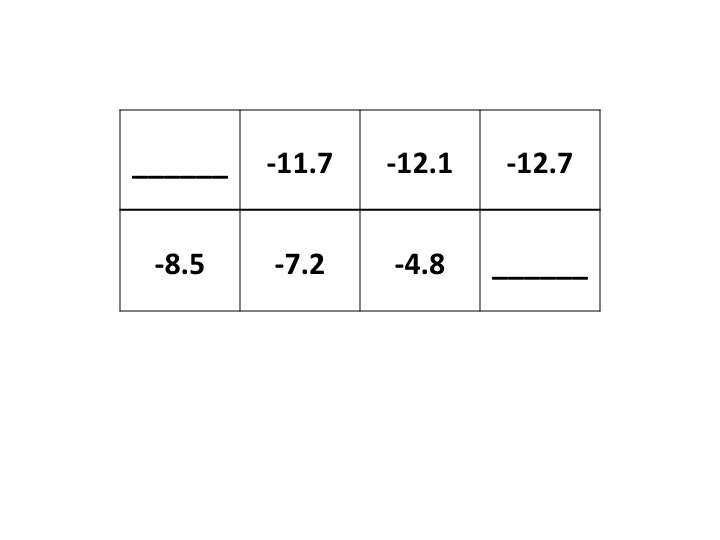
(c) Policy (15 pts)
Given the value function Vπ computed in (b),
what new policy π' would policy iteration produce at
the next iteration? Show your answer as a diagram (arrows
on the grid) or as a state-action table.
Explain how you arrived at your answer!