NOTE about deadlines: If you wish, you may turn part or
all of this homework by class time on Thursday 3/13 (before
spring break). If you do so, then that part of the homework
will be returned to you, graded, by Thursday 3/27 at the latest,
so that you have it available as a study resource before the
midterm.
As stated in the course syllabus, you are permitted (nay, encouraged!) to work on this homework assignment in groups of up to three students. If you work in a group, you only need to turn in one shared solution, with everyone's name on the assignment. All students in the group will receive the same grade on the assignment. If you choose to work in a group, you must actually produce group solutions, not have each member work independently on one part of the assignment, then submit the collection of independent solutions.
(b) (10 points) Russell & Norvig Exercise 3.26 (a-e only).
For example, if Player 1's coin lands tails up, she gets two points. Player 2 then takes her turn, gets heads, and now has one point. Player 1 decides to stop the game, and wins, beating Player 2 by one point.
Draw the 4-ply expectiminimax tree for this problem (two moves for each player). Using the static evaluation function (score(player1) - score(player2)), back up the leaf values to the root of the tree. What is the best action for the first player to take? (Play or stop?) If player 1 flips tails, what should player 2 do? Why?
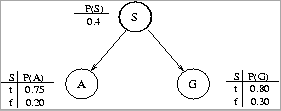
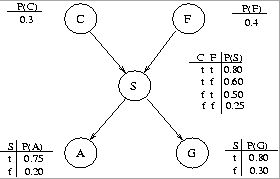
(a) (3 pts) Compute P(a, ~s, g) using the chain rule.
(b) (4 pts.) Compute P(a) using inference by enumeration.
(c) (5 pts.) Using conditional independence, compute P(~g, a | s) and P(~g, a | ~s). Then use Bayes' rule to compute P(s | ~g, a).(d) (3 pts.) The enterprising student notices that two types of
people drive SUVs: people from California (C) and people with large families
(F). After collecting some statistics, the student arrives at the BN:

Using the chain rule, compute the probability P(~g, a, s, c, ~f).
(e) (5 pts) Write, in summation form, the formula for computing
P(a, ~f) using inference by enumeration. (You do not need to
actually compute the probability.)
(h) (5 pts) Using the rules for determining when two variables are (conditionally) independent of each other in a BN, answer the following (T/F) for the BN given in (c):
(a) Iterated Prisoner's Dilemma (5 pts)
| C | D | |
| C | 3,3 | 0,5 |
| D | 5,0 | 1,1 |
(b) Rock-Paper-Scissors (5 pts)
Also called "Roshambo," each player chooses to present one of three objects: rock, paper, or scissors. Rock breaks (beats) scissors; paper covers (beats) rock; scissors cuts (beats) paper. Nobody wins (it's a tie) if both players pick the same object.
| R | P | S | |
| R | 0,0 | -1,+1 | +1,-1 |
| P | +1,-1 | 0,0 | -1,+1 |
| R | -1,+1 | +1,-1 | 0,0 |
(c) Chicken (5 pts)
Two drivers are headed for a one-lane bridge. If they both swerve out of the way, they "tie" (nobody scores). If one swerves and the other drives straight on, the "chicken" loses a point and the gutsy driver gains a point. If neither swerves, they both lose big.
| Straight | Swerve | |
| Straight | -10,-10 | +1,-1 |
| Swerve | -1,+1 | 0,0 |
State the Nash equilibria of your game and explain why they are the equilibria. Also indicate what the social welfare maximizing strategy sets are for your game. Will rational players maximize social welfare in your game?
Do you think that the "tit-for-tat" strategy, which has been used successfully with the IPD, would work well for a player in your game? Why or why not?