Introduction to Artificial Intelligence

Homework #6

December 7th at 2:30pm

In this homework assignment you will gain familiarity with WEKA, the Waikato Environment for Knowledge Analysis. WEKA is widely used in the machine learning and data mining communities because, among other things, it provides both a nice user interface to a number of standard algorithms and a Java API. You will also solidify what you learned about decision trees and nearest neighbor classifiers in class by experimenting with them on real and artificial data.

Download WEKA

First, you must download WEKA from the following URL: http://www.cs.waikato.ac.nz/ml/weka/. The "Getting Started" section of that page has links for information on system requirements, how to download the software, and documentation. WEKA is written in Java and should run on any platform with Java 1.5 or higher.

Write a Dataset Generator

Write a simple program in any language you like to generate data (training instances) for use by WEKA. You will use the output of the data generator in the experiments below.

Each instance should consist of some number of binary attributes, whose values are assigned at random, and a binary class label, whose value is determined by a boolean function of your choice and is corrupted by noise with some probability. Your program should take at least the following parameters:

N - number of instances to generate.
M - number of attributes per instance. Note that M must be no smaller than the number of attributes required to compute the class label.
P - probability of noise in the class attribute. After computing the true class label for each instance, toggle the class label with probability P. On average, PN of the N instances will have the wrong class label.

Be sure the output of your program is in the format expected by WEKA, which is called ARFF. See the doccumentation mentioned above for more information on this format. Also, there are several sample data files in the data directory of the WEKA distribution.

Exploring a Dataset

When you first run WEKA, choose the Explorer button. Open a dataset in the data directory of the WEKA distribution. Use the visualizations available from the Preprocess and Visualize sub-systems of the Explorer to gain a better understanding of the relationships between the attributes and between the attributes and the class label.

What to submit: Write a couple of paragraphs describing some of the structure you found in the dataset.

Exploring Decision Trees

In the Classify sub-system of the Explorer, use the J48 decision tree algorithm to learn a decision tree for the dataset you just explored. This is the WEKA implementation of C4.5.

What to submit: Submit the output of the classifier on your dataset and describe, in words, what structure the decision tree found in the data.

Using your data generator, explore the impact of dataset size, number of irrelevant attributes, and noise on the ability of J48 to learn a good decision tree. Try to find a dataset for which the decision tree perfectly captures the function you used to assign class labels.

What to submit: Write a few paragraphs summarizing your observations on how features of the dataset impact the learned decision trees and, in particular, whether or not the trees are overfit. Submit the "best" decision tree you were able to obtain using J48.

Exploring Nearest Neighbor

Repeat the artificial data experiments with the IB1 (1-nearest neighbor) classifier.

What to submit: Write a couple of paragraphs summarizing your observations on how features of the dataset impact accuracy of the IB1 classifier. Also compare/contrast the performance of IB1 and J48.

Decision Tree Exercise

Consider the following decision tree:

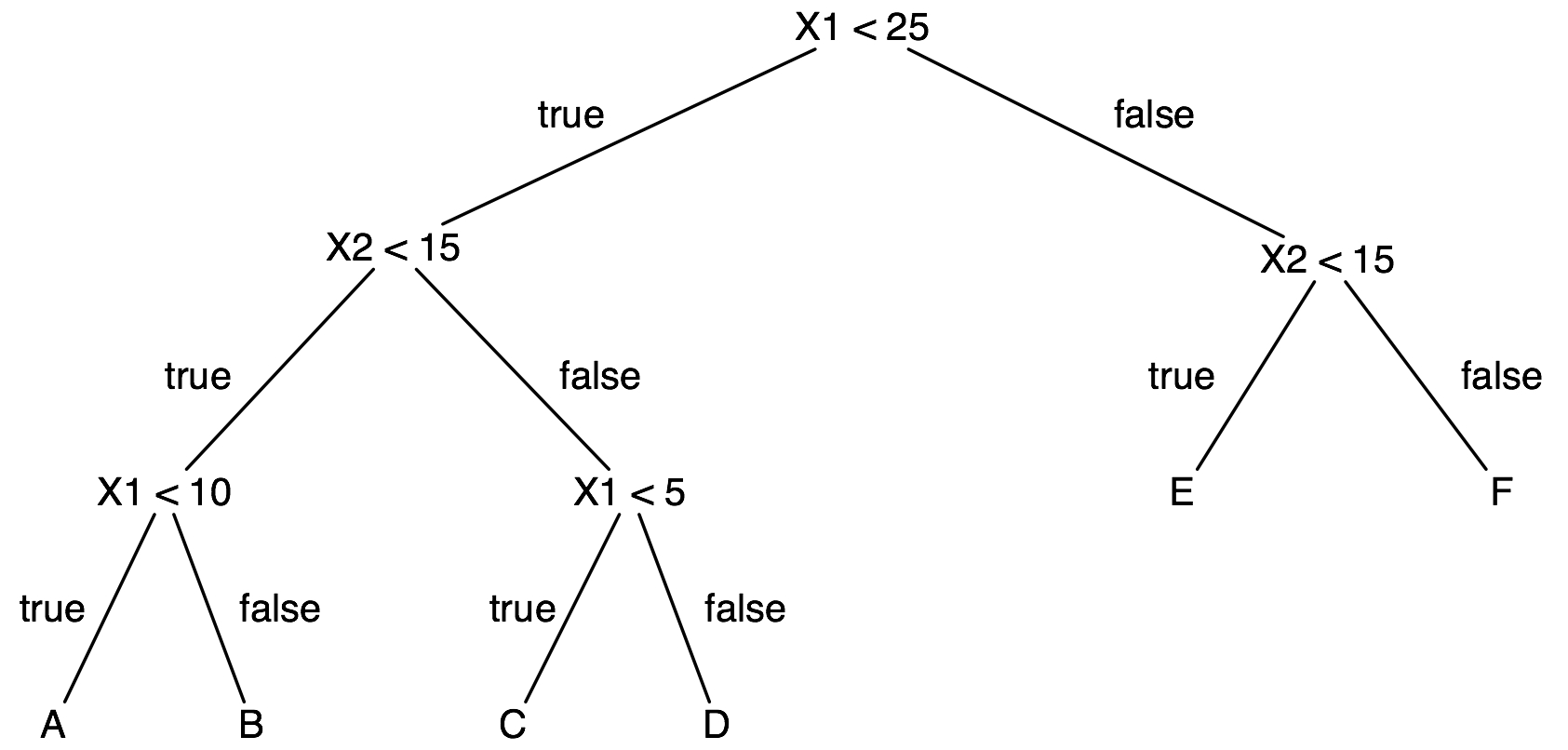
(A) Draw the decision boundaries defined by this tree. That is, draw in the plane defined by X1 and X2 the rectangular regions corresponding to the subset of the instance space covered by each leaf. Each leaf is labeled with a letter. Write this letter in the corresponding region of instance space.

(B) Give another decision tree that is syntactically different but defines the same decision boundaries. This demonstrates that the space of decision trees is syntactically redundant.

Nearest Neighbor Exercise

Consider the following training set:

(A) Draw the decision boundary for the 1-nearest neighbor algorithm assuming that we are using standard Euclidean distance to compute nearest neighbors.

(B) How will the point (8, 1) be classified?

(C) How will the point (8, 8) be classified?

Bayesian Reasoning (10 points extra credit)

The Monty Hall problem is as follows: You are on a game show and the host presents you with three doors. Behind one is a car and behind the other two are goats. You choose a door. Regardless of whether your door has the car or a goat, there is at least one other door with a goat. The host opens such a door and shows you a goat. He then asks "would you like to stay with the door you chose or switch to the other door". If you want to maximize your chances of winning the car, should you switch?

This problem is famous for confounding lots of very smart people who say that it makes absolutely no difference whether you switch or not. The reasoning is that opening a door with a goat doesn't change the probability that the car is behind the door you initially chose. It's still 1/3.

It turns out that it is best to switch!

Your assignment is to present a Bayesian argument as to why this is the case. Feel free to use external resources (like the web), but I want you to submit a short writeup based on the application of Bayes rule that is entirely your own. Read and understand the arguments, but write them up in your own words.