CMSC 471 - Homework #6

I. Decision tree learning (25 pts.)

1. Information Gain (10 pts.) At the root node for a decision tree in this domain, what are the information gains associated with the Outlook and Humidity attributes? (Use a threshold of 75 for humidity (i.e., assume a binary split: humidity <= 75 / humidity > 75.)

2. Gain Ratios (10 pts.) Again at the root node, what are the gain ratios associated with the Outlook and Humidity attributes (using the same threshold as in (a))?

3. Decision Tree (5 pts.) Suppose you build a decision tree that splits on the Outlook attribute at the root node. How many children nodes are there are at the first level of the decision tree? Which branches require a further split in order to create leaf nodes with instances belonging to a single class? For each of these branches, which attribute can you split on to complete the decision tree building process at the next level (i.e., so that at level 2, there are only leaf nodes)? Draw the resulting decision tree, showing the decisions (class predictions) at the leaves.
    

   II. SVMs and Kernel Spaces (25 pts)

   I'm looking for a paragraph or so on each of these questions, not a lengthy exposition on every aspect of the methods.
   1. Linear Models (8 pts) Linear SVMs and decision trees both learn linear separators in the instance space. Do they therefore have the same model space? If so, explain why these two approaches differ in the way they search the model space. If not, explain what the main differences are between the two model spaces.
   2. Kernel Basis Functions (8 pts) What are kernel basis functions used for in SVM learning? How do they change the model space of the learner?
   3. Basis Functions and Decision Trees (9 pts) Supppose that one incorporated a set of kernel basis functions -- say, low-order polynomials -- into the feature space for a decision tree. Would the model space then look the same as that of an SVM in that kernel space? Why or why not?

   III. MDPs and RL (25 pts)

   The diagram below shows a gridworld domain in which the agent starts at the upper left location. The upper and lower rows are both "one-way streets," since only the actions shown by arrows are available.

   Actions that attempt to move the agent into a wall (the outer borders, or the thick black wall between all but the leftmost cell of the top and bottom rows) leave the agent in the same state it was in with probability 1, and have reward -2. If the agent tries to move to the right from the upper right or lower right locations, with probability 1, it is teleported to the far left end of the corresponding row, with reward as marked. All other actions have the expected effect (move up, down, left, or right) with probability .9, and leave the agent in the same state it was in with probability .1. These actions all have utility -1, except for the transitions that are marked. (Note that the marked transitions only give the indicated reward if the action succeeds in moving the agent in that direction.)
   
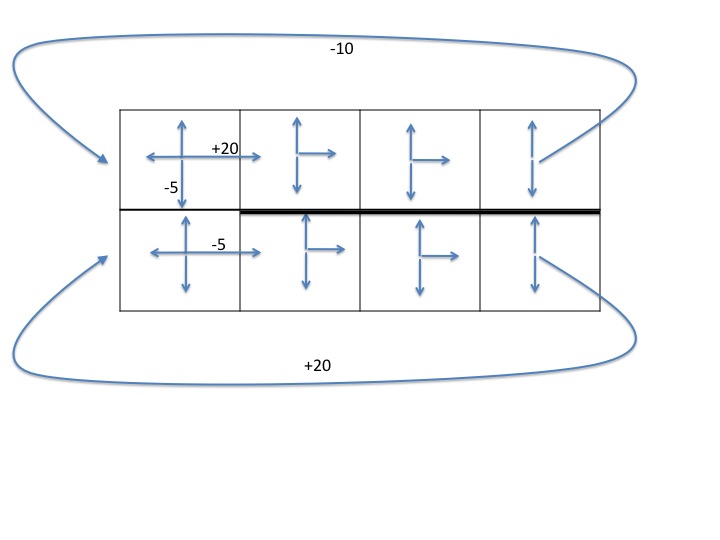
   (a) MDP (10 pts) Give the MDP for this domain only for the state transitions starting from each of the states in the top row, by filling in a state-action-state transition table (showing only the state transitions with non-zero probability). You should refer to each state by its row and column index, so the upper left state is [1,1] and the lower right state is [2,4].

   To get you started, here are the first few lines of the table:

   State s	Action a	New state s'	p(s'|s,a)	r(s,a,s')
   [1,1]	Up	[1,1]	1.0	-2
   [1,1]	Right	[1,1]	0.1	-1
   [1,1]	Right	[1,2]	0.9	+20

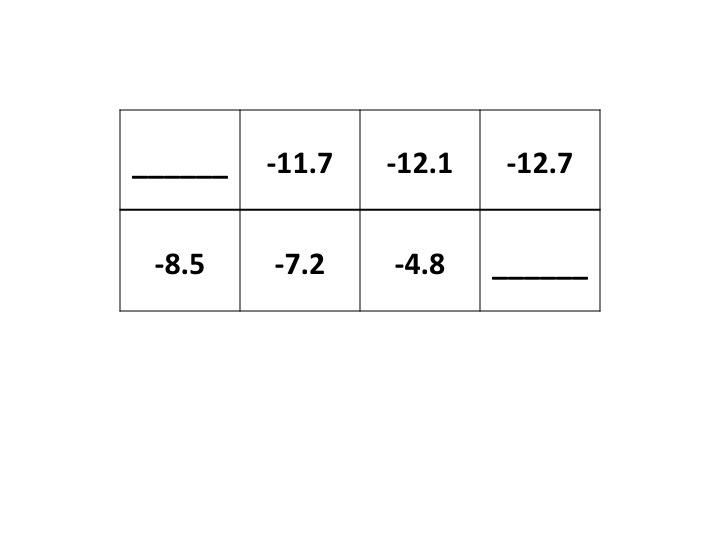
   (b) Value function (8 pts) Suppose the agent follows a randomized policy π (where each available action in any given state has equal probability) and uses a discount factor of γ=.85. Given the partial value function (V^π; U^π in Russell & Norvig's terminology) shown below, fill in the missing V^π values. Show and explain your work.
   
   (c) Policy (7 pts) Given the value function V^π computed in (b), what new policy π' would policy iteration produce at the next iteration? Show your answer as a diagram (arrows on the grid) or as a state-action table.

IV. Multi-Agent Systems (25 pts)

1. Game Analysis (12 pts) For each of the three normal-form two-player games below, identify the Nash equilibria (if there are any). Explain why these strategy sets are the Nash equilibria of the game, or why no Nash equilibria exist if this is the case. Also indicate the social-welfare-maximizing strategy sets for each game. Given the Nash equilibria that you've identified, will rational players choose the social-welfare-maximizing strategy set?

   (a) Iterated Prisoner's Dilemma (4 pts)

   	C	D
   C	3,3	0,5
   D	5,0	1,1

   (b) Rock-Paper-Scissors (4 pts)

   Also called "Roshambo," each player chooses to present one of three objects: rock, paper, or scissors. Rock breaks (beats) scissors; paper covers (beats) rock; scissors cuts (beats) paper. Nobody wins (it's a tie) if both players pick the same object.

   	R	P	S
   R	0,0	-1,+1	+1,-1
   P	+1,-1	0,0	-1,+1
   R	-1,+1	+1,-1	0,0

   (c) Chicken (4 pts)

   Two drivers are headed for a one-lane bridge. If they both swerve out of the way, they "tie" (nobody scores). If one swerves and the other drives straight on, the "chicken" loses a point and the gutsy driver gains a point. If neither swerves, they both lose big.

   	Straight	Swerve
   Straight	-10,-10	+1,-1
   Swerve	-1,+1	0,0

2. Game Creation (13 points) Create your own game for two or more players by specifying a normal form table. Explain the game in English (you don't have to have a great story, but it shouldn't just consist of random payoffs).

   State the Nash equilibria of your game and explain why they are the equilibria. Also indicate what the social welfare maximizing strategy sets are for your game. Will rational players maximize social welfare in your game?

   Do you think that the "tit-for-tat" strategy, which has been used successfully with the IPD, would work well for a player in your game? Why or why not?