CMSC 471 - Fall 2009 - Homework #5

1. Planning Representations (25 pts.)

Our agent is hungry and unhappy, and wants to go on a vacation, sunbathe, and eat well. Our agent starts out rich, but only has limited options, some of which will consume a substantial part of its wealth.

• The static predicates for the domain are:

  	have(car)	The agent has a car
  	distance(x,y,d)	The distance from x to y is d; distance is assumed to be reflexive; i.e., distance(x,y,d) <=> distance(y,x,d)
  	temp(x,t)	The temperature at location x is t
  	in(r,x)	Restaurant r is in city x
  	beach(x)	There is a beach in location x
  	fastfood(r)	r is a fast-food restaurant
  	swanky(r) r is a swanky restaurant

• The dynamic predicates for the domain are:

  	at(x,s)	The agent is at x in situation s
  	happy(s)	The agent is happy in situation s
  	hungry(s)	The agent is hungry in situation s
  	rich(s)	The agent is rich in situation s

  (Note that the situation variables will only be used in part (a) of this problem.)
• The constants in the domain are:

  	Balt	Baltimore
  	Berm	Bermuda
  	OC	Ocean City
  	McDs	McDonald's
  	BK	Burger King
  	CTC	Chez Tres Cher
  	MC	Molto Caro

• The initial state is:
  • at(Balt, s0) ^ ~happy(s0) ^ hungry(s0) ^ rich(s0).
• The static predicates in the KB are:
  • distance (Balt,OC,150)
  • distance(Balt,Berm,500)
  • in(McDs,Berm)
  • in(BK,OC)
  • in(CTC,Berm)
  • in(MC,OC)
  • fastfood(McDs)
  • fastfood(BK)
  • swanky(CTC)
  • swanky(MC)
  • have(car)
  • beach(OC)
  • beach(Berm)
  • temp(Balt,50)
  • temp(OC,60)
  • temp(Berm,80)
• The actions in the domain are as follows:
  • drive(x,y) : The agent can drive from location x to location y if it has a car and the distance from x to y is less than or equal to 200.
  • fly(x,y) : The agent can fly from location x to location y if it is rich and the distance from x to y is greater than 200. Flights are expensive, so after flying, the agent is no longer rich.
  • sunbathe(x) The agent can sunbathe if it is in a location (x) with a beach. The agent will end up happy after sunbathing if the temperature is above 75, but unhappy if the temperature is below 75.
  • eat(r): If the agent is hungry [i.e., hunger is a precondition], it can eat at a restaurant r that is In the same location as the agent. The agent will end up not hungry, and will be happy if the restaurant is a swanky restaurant. However, it can only eat at a swanky restaurant if it is rich, and at the end of the action, will not be rich any more. (Fast food restaurants don't require richness, and don't change the status of the richness predicate.)

(a) (7 pts.) Describe only the Happy predicate using the situation calculus. You should have one or more possibility axioms (one for each relevant action)  and one or more successor-state axioms (one for each relevant action). These axioms should characterize how the state of the Happy predicate changes as a result of the actions in the domain, in terms of the domain predicates listed above. (You may want to refer to pages 330-333 in the book.)

(b) (7 pts.) Describe the actions in this domain as STRIPS operators. Be sure to include all preconditions, add lists, and delete lists.  (See pages 377-378.)

(c) (5 pts.) Show two different legal plans (sequences of actions) for achieving the goal described above from the given initial state.

(d) (6 pts.) How many legal plans are there for this goal? Explain your answer.  Does the answer change depending on whether or not repeated states are allowed?

2. Partial-Order Planning (25 pts.)

Now suppose that the agent decides to satisfy its Happiness goal using the Sunbathe action. Insert this action into the plan, showing all dependencies. Will this plan succeed? If so, complete the partial plan, resolving any threats that arise. If not, complete the partial plan to the point where planning fails, and explain the source of the failure.

3. Bayesian networks and probability (50 pts.)

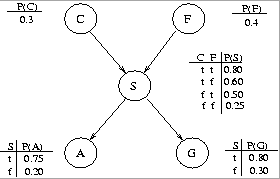
(a) (5 pts) Compute P(a, ~s, g) using the chain rule.

(b) (8 pts.) Compute P(a) using inference by enumeration.

(d) (5 pts.) The enterprising student notices that two types of people drive SUVs: people from California (C) and people with large families (F). After collecting some statistics, the student arrives at the BN:

Using the chain rule, compute the probability P(~g, a, s, c, ~f).

(e) (5 pts) Write, in summation form, the formula for computing P(a, ~f) using inference by enumeration.  (You do not need to actually compute the probability.)

(f) (4 pts) What is the conditional independence assumption for a node in a BN?

(g) (4 pts) When are two variables conditionally independent of each other in a BN?

(h) (10 pts) Using the rules for determining when two variables are (conditionally) independent of each other in a BN, answer the following (T/F) for the BN given in (c):

1. I(C,G)
2. I(F,A | S)
3. I(C,F)
4. I(C,F | S)
5. I(C,F | A)