CMSC 471 - Homework #6

1. Planning Representations (25 pts.)

Our agent is hungry and unhappy, and wants to go on a vacation, sunbathe, and eat well. Our agent starts out rich, but only has limited options, some of which will consume a substantial part of its wealth.

• The static predicates for the domain are:
  • have(car)                   (The agent has a car)
  • distance(x,y,d)          (The distance from x to y is d; distance is assumed to be reflexive; i.e., distance(x,y,d) <=> distance(y,x,d))
  • temp(x,t)                    (The temperature at location x is t)
  • in(r,x)                          (Restaurant r is in city x)
  • beach(x)                    (There is a beach in location x)
  • fastfood(r)                  (r is a fast-food restaurant)
  • swanky(r)                   (r is a swanky restaurant)
• The dynamic predicates for the domain are:
  • at(x,s)                        (The agent is at x in situation s)
  • happy(s)                    (The agent is happy in situation s)
  • hungry(s)                   (The agent is hungry in situation s)
  • rich(s)                        (The agent is rich in situation s)
• (Note that the situation variables will only be used in part (a) of this problem.)
• The constants in the domain are:
  • Balt                           (Baltimore)
  • Berm                        (Bermuda)
  • OC                            (Ocean City)
  • McDs                        (McDonald's)
  • BK                             (Burger King)
  • CTC                          (Chez Tres Cher)
  • MC                            (Molto Caro).
• The initial state is:
  • at(Balt, s0) ^ ~happy(s0) ^ hungry(s0) ^ rich(s0).
• The static predicates in the KB are:
  • distance (Balt,OC,150)
  • distance(Balt,Berm,500)
  • in(McDs,Berm)
  • in(BK,OC)
  • in(CTC,Berm)
  • in(MC,OC)
  • fastfood(McDs)
  • fastfood(BK)
  • swanky(CTC)
  • swanky(MC)
  • have(car)
  • beach(OC)
  • beach(Berm)
  • temp(Balt,50)
  • temp(OC,60)
  • temp(Berm,80)
• The actions in the domain are as follows:
  • drive(x,y) : The agent can drive from location x to location y if it has a car and the distance from x to y is less than or equal to 200.
  • fly(x,y) : The agent can fly from location x to location y if it is rich and the distance from x to y is greater than 200. Flights are expensive, so after flying, the agent is no longer rich.
  • sunbathe(x) The agent can sunbathe if it is in a location (x) with a beach. The agent will end up happy after sunbathing if the temperature is above 75, but unhappy if the temperature is below 75.
  • eat(r): If the agent is hungry [i.e., hunger is a precondition], it can eat at a restaurant r that is In the same location as the agent. The agent will end up not hungry, and will be happy if the restaurant is a swanky restaurant. However, it can only eat at a swanky restaurant if it is rich, and at the end of the action, will not be rich any more. (Fast food restaurants don't require richness, and don't change the status of the richness predicate.)

(a) (7 pts.) Describe only the Happy predicate using the situation calculus. You should have one or more possibility axioms (one for each relevant action)  and one or more successor-state axioms (one for each relevant action). These axioms should characterize how the state of the Happy predicate changes as a result of the actions in the domain, in terms of the domain predicates listed above.
(You may want to refer to pages 330-333 in the book.)

(b) (7 pts.) Describe the actions in this domain as STRIPS operators. Be sure to include all preconditions, add lists, and delete lists.  (See pages 377-378.)

(c) (5 pts.) Show two different legal plans (sequences of actions) for achieving the goal described above from the given initial state.

(d) (6 pts.) How many legal plans are there for this goal? Explain your answer.  Does the answer change depending on whether or not repeated states are allowed?

2. Partial-Order Planning (25 pts.)

Now suppose that the agent decides to satisfy its Happiness goal using the Sunbathe action. Insert this action into the plan, showing all dependencies. Will this plan succeed? If so, complete the partial plan, resolving any threats that arise. If not, complete the partial plan to the point where planning fails, and explain the source of the failure.

3. Decision tree learning (25 pts.)

(a) (10 pts.) At the root node for a decision tree in this domain, what are the information gains associated with the Outlook and Humidity attributes? (Use a threshold of 75 for humidity (i.e., assume a binary split: humidity <= 75 / humidity > 75.)

(b) (10 pts.) Again at the root node, what are the gain ratios associated with the Outlook and Humidity attributes (using the same threshold as in (a))?

(c) (5 pts.) Suppose you build a decision tree that splits on the Outlook attribute at the root node. How many children nodes are there are at the first level of the decision tree? Which branches require a further split in order to create leaf nodes with instances belonging to a single class? For each of these branches, which attribute can you split on to complete the decision tree building process at the next level (i.e., so that at level 2, there are only leaf nodes)? Draw the resulting decision tree, showing the decisions (class predictions) at the leaves.
 

4. Version spaces (25 points)

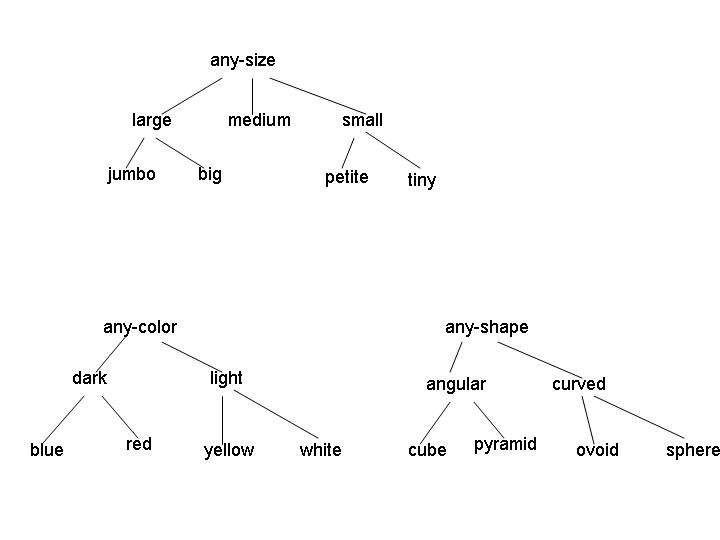
Examples of legal concepts in this domain include [medium light angular], [large red sphere], and [any-size any-color any-shape]. No disjunctive concepts are allowed, other than the implicit disjunctions represented by the internal nodes in the attribute hierarchies.  (For example, the concept [large [red v yellow] curved] isn't allowed.)

(a) (5 points) Consider the initial version space for learning in this domain.  What is the G set?  How many elements are in the S set? Give one representative member of the initial S set.

(b) (5 points) Suppose the first instance I1 is a positive example, with attribute values [jumbo yellow ovoid]. After processing this instance, what are the G and S sets?

(c) (5 points) Now suppose the learning algorithm receives instance I2, a negative example, with attribute values [jumbo red pyramid]. What are the G and S sets after processing this example?

(d) (10 points - 2.5 points each) For this question, you should start with the version space that remains after I1 and I2 are processed. For each of the following combinations of instance type and events, give a single instance of the specified type that would cause the indicated event, if such an instance exists. If no such instance exists, explain why.

1. A positive instance that causes the version space to collapse.
2. A negative instance that causes the version space to collapse.
3. A positive instance that reduces the size of the version space to a single concept.
4. A negative instance that reduces the size of the version space to a single concept.

Bonus: (e) (5 points) If learning ends after I1 and I2 are processed, how many concepts remain in the version space?