CMSC 471 - Homework #5

Out 10/28/04, due 11/11/04

1. Probability warm-up (20 pts.)

(R&N 14.5) Using only the basic laws of probability theory (the three axioms of probability, the definition of conditional probability, the product rule, and/or Bayes' rule), prove the following theorems:

(a) (10 pts.) Prove the conditionalized version of the general product rule:

P(A ^ B | E) = P(A | B ^ E) P(B | E)

(b) (10 pts.) Prove the conditionalized version of Bayes' rule:

P(A | B ^ C) = P(B | A ^ C) P(A | C) / P(B | C)

2. Bayesian networks and probability (55 pts.)

A CMSC 471 student notices that people who drive SUVs (S) consume large amounts of gas (G) and are involved in more
accidents (A) than the national average. She has constructed the following Bayesian network:

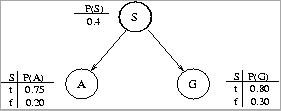
(a) (5 pts) Compute P(a, ~s, g) using the chain rule.

(b) (10 pts.) Compute P(a) using inference by enumeration.

(c) (10 pts.) Using conditional independence, compute P(~g, a | s) and P(~g, a | ~s). Then use Bayes' rule to compute P(s | ~g, a).

(d) (5 pts.) The enterprising student notices that two types of people drive SUVs: people from California (C) and people with large families (F). After collecting some statistics, the student arrives at the following form for the BN:

Using the chain rule, compute the probability P(~g, a, s, c, ~f).

(e) (5 pts) Write, in summation form, the formulat for computing P(a, ~f) using inference by enumeration. (You do not need to actually compute the probability.)

(f) (4 pts) What is the conditional independence assumption for a node in a BN?

(g) (4 pts) When are two variables conditionally independent of each other in a BN?

(h) (12 pts) Using the rules for determining when two variables are (conditionally) independent of each other in a BN, answer the following (T/F) for the BN given in (c):

I(C,G)
I(F,A | S)
I(C,F)
I(A,G)
I(C,F | S)
I(C,F | A)

3. Semantic Networks (25 pts.)

Represent the following KB using a semantic network:

201 is a programming class.
202 is a programming class.
341 is a programming class.
341 is a theory class.
STAT 355 is a statistics class.
441 is a theory class.
471 is an AI class.
477 is an AI class.
Programming, theory, and AI classes are all computer science classes.
Prerequisites are as follows: 201 < 202 < 341 < 471.
Recommended class orders are as follows: 441 < 471, STAT 355 < 471, 471 < 477.
Computer science classes are hard.
Programming classes are easy.
Theory classes are hard.

How would a semantic network be used to answer the following questions? Discuss how alternative implementations might yield different answers, and what other information might be needed in order to provide an unambiguous question.

Is 471 hard?
Is 341 hard?
Is STAT 355 hard?
Is 201 a prerequisite for 471?