Please remember: In all questions on this homework (and throughout
the class!), you should show your reasoning, in order to receive partial
credit for incorrect answers.
(a) (5 points) Let the constant CC denote a credit card that the agent can use to buy any object. Modify the description of Buy so that the agent has to have its credit card in order to buy anything. Note that you will also need to modify the At predicate so that it takes two arguments: an object (e.g., the agent or the credit card) and a location.
(b) (6 points) Write a PickUp operator that enables the agent to Have an object if it is portable and at the same location as the agent.
(c) (12 points) Assume that the credit card is At home, but Have(CC) is initially false. Show a partially ordered plan that achieves the (simplified) goal (of Have(Milk) & At(Home)), showing both ordering constraints and causal links. (Note that we are no longer worrying about bananas and drills, just milk. Note also that you only need to show the plan, not the planning steps.)
(d) (12 points) Explain in detail what happens during the planning process
when the agent explores the partial plan constructed in (c) in which it
leaves home without the card. (You can do this by showing a series of partial
plans in the search sequence, or by listing the sequence of plan modifications
and/or backtracking steps using clear and complete English descriptions.)
| Outlook | Temp (F) | Humidity (%) | Windy? | Class |
| sunny | 75 | 70 | true | Play |
| sunny | 80 | 90 | true | Don't Play |
| sunny | 85 | 85 | false | Don't Play |
| sunny | 72 | 95 | false | Don't Play |
| sunny | 69 | 70 | false | Play |
| overcast | 72 | 90 | true | Play |
| overcast | 83 | 78 | false | Play |
| overcast | 64 | 65 | true | Play |
| overcast | 81 | 75 | false | Play |
| rain | 71 | 80 | true | Don't Play |
| rain | 65 | 70 | true | Don't Play |
| rain | 75 | 80 | false | Play |
| rain | 68 | 80 | false | Play |
| rain | 70 | 96 | false | Play |
(a) (10 pts.) At the root node for a decision tree in this domain, what are the information gains associated with the Outlook and Humidity attributes? (Use a threshold of 75 for humidity (i.e., assume a binary split: humidity <= 75 / humidity > 75.)
(b) (10 pts.) Again at the root node, what are the gain ratios associated with the Outlook and Humidity attributes (using the same threshold as in (a))?
(c) (10 pts.) Suppose you build a decision tree that splits on the Outlook
attribute at the root node. How many children nodes are there are at the
first level of the decision tree? Which branches require a further split
in order to create leaf nodes with instances belonging to a single class?
For each of these branches, which attribute can you split on to complete
the decision tree building process at the next level (i.e., so that at
level 2, there are only leaf nodes)? Draw the resulting decision tree,
showing the decisions (class predictions) at the leaves.

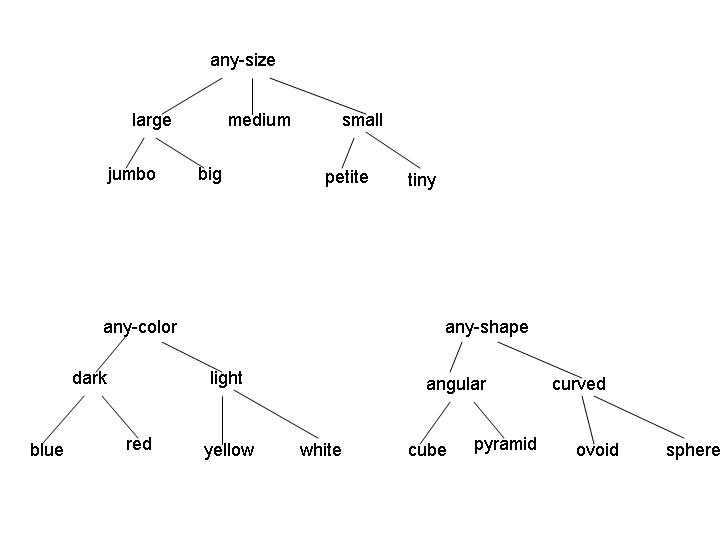
Examples of legal concepts in this domain include [medium light angular], [large red sphere], and [any-size any-color any-shape]. No disjunctive concepts are allowed, other than the implicit disjunctions represented by the internal nodes in the attribute hierarchies. (For example, the concept [large [red v yellow] curved] isn't allowed.)
(a) (5 points) Consider the initial version space for learning in this domain. What is the G set? How many elements are in the S set? Give one representative member of the initial S set.
(b) (5 points) Suppose the first instance I1 is a positive example, with attribute values [jumbo yellow ovoid]. After processing this instance, what are the G and S sets?
(c) (5 points) Now suppose the learning algorithm receives instance I2, a negative example, with attribute values [jumbo red pyramid]. What are the G and S sets after processing this example?
(d) (4 points) If learning ends at this point, how many possible concepts remain in the version space?
(e) (16 points - 4 points each) For this question, you should start with the version space that remains after I1 and I2 are processed. For each of the following combinations of instance type and events, give a single instance of the specified type that would cause the indicated event, if such an instance exists. If no such instance exists, explain why.