Midterm Review¶

Disclaimer:¶

Appearing on this page does not mean something will be on the test
Not appearing on this page does not mean something won't be on the test

Context-Free Grammars (BNF)¶

How to read BNF and write simple grammars
How to do a derivation
How to construct a parse tree
Ambuigity
- Operator Precedence and Associativity
EBNF
The basics of attribute grammars
- What problems they are meant to solve

Writing a BNF Practice¶

Write the BNF for a local variable decleration in Java

$ < dec > \to < type > < names > ; $
$ < type > \to < object > | < primitive > | < object > [] | < primitive > [] $
$ < primitive > \to $ int | float | boolean | char | ....
$ < names > \to < name > | < name > , < names > $

Derivations and Parse Trees¶

Given the following grammar:

$< assign > \to < id > = < expr > $
$< id > \to A \, | \, B \, | \, C $
$< expr > \to < expr > + < expr> $
$\qquad \qquad | < expr > * < expr> $
$\qquad \qquad | \, ( < expr> ) $
$\qquad \qquad | < id > $

Derive and give the parse trees for:

B = A + C
C = (A * C) + B

For B = A + C

$< assign > \Rightarrow < id > = < expr > $

$ \qquad \qquad \Rightarrow B = < expr > $

$ \qquad \qquad \Rightarrow B = < expr > + < expr > $

$ \qquad \qquad\Rightarrow B = < id > + < expr > $

$ \qquad \qquad \Rightarrow B = A + < expr > $

$ \qquad \qquad \Rightarrow B = A + < id > $

$ \qquad \qquad \Rightarrow B = A + C $

For C = (A * C) + B,

$< assign > \Rightarrow < id > = < expr > $
$ \qquad \qquad \Rightarrow C = < expr > $
$ \qquad \qquad \Rightarrow C = < expr > + < expr > $
$ \qquad \qquad\Rightarrow C = ( < expr > ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( < expr > * < expr > ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( < id > * < expr > ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( A * < expr > ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( A * < id > ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( A * C ) + < expr > $
$ \qquad \qquad\Rightarrow C = ( A * C ) + < id > $
$ \qquad \qquad\Rightarrow C = ( A * C ) + B $

Semantics¶

Operational Semantics
Denotational Semantics
Axiomatic Semantics

Misc BNF¶

Given the following grammar:

$< assign > \to < id > = < expr > $
$< id > \to A \, | \, B \, | \, C $
$< expr > \to < expr > + < term > $
$\qquad \qquad | < term > $
$< term > \to < term > * < factor > $
$ \qquad \qquad | < factor > $
$< factor > \to ( < expr> ) $
$\qquad \qquad | < id > $

Is this grammar unambiguous: No
What is the precedence of () , * , + ?: () has higest, followed by *, followed by +
What is the associativity of * and +?: Both are left associative

Operational and Denotional Semantics¶

Operational Semantics is describing the semantics of a language by state changes
- Usually uses abstract machine code
Denotational Semantics is describing semantics as mathmateical objections

For the grammar:

$ < dec\_num > \to$ '0' | '1' | '2'| '3' | '4' | '5' | '6' | '7' | '8' | '9'
$ \qquad \qquad \quad \, \, \,$ | $< dec\_num>$ ('0' | '1' | '2'| '3' | '4' | '5' | '6' | '7' | '8' | '9')

The denotational mappings are:

$M_{dec}$('0') = 0, $M_{dec}$('1') = 1, $M_{dec}$('2') = 2, ... , $M_{dec}$('9') = 9
$M_{dec}$( $< dec\_num >$ '0') = 10 * $M_{dec}$( $< dec\_num >$)
$M_{dec}$( $< dec\_num >$ '1') = 10 * $M_{dec}$( $< dec\_num >$) + 1
...
$M_{dec}$( $< dec\_num >$ '9') = 10 * $M_{dec}$( $< dec\_num >$) + 9

Axiomatic Semantics¶

Originally intended for program verification
Solve the following:

Compute weakest precondition

a = 3 * ( 2 * b + a);
b = 2 * a - 1;
{ b > 5}

$ \frac{1 - a}{b} < 2$

x = 2 * y + x - 1;
{ x > 11}

$ \frac{12-x}{y} < 12 $

if x < 0 then
    y = y - 1
else
    y = y + 1

{y > 0}

$y > 1$

Parsing and Lexical Analysis¶

Regular Expressions
- How to read and write basic regular expressions
- How they are used in lexical analysis
Deterministic Finite Automata
- How to read and write basic DFAs
- How they are used in lexical anyalsis
- Their relationship with Regular Expressions
Top Down Parsing
- The gist of how its implemented
- Problems it cannot handle
Bottom Up Parsing
- What are the advantages of it
- How to trace a shift reduce parse of a string given a parsing table

Regular Expressions¶

Find the regular expressions for:

an IP address
- [0-9][0-9][0-9].[0-9][0-9][0-9].[0-9][0-9][0-9].[0-9][0-9][0-9]
A word that is capitalized
- [A-Z][a-z]*
A word ending in -ing or -ed
- [a-z]+(ing|ed)

DFAs¶

Write the DFAs for:

an IP address
A word that is capitalized
A word ending in -ing or -ed

Top-Down Parsing¶

Sketch out the top down parsing function for the rule $ T \to T * F $

T(){
    T()
    while next_token == '*'{
        F()
    }
}

Bottom-Up Parsing¶

Show the parse including the stack for id + id

Grammar:

$E \to E \, + \, T$
$E \to T$
$T \to T \, * \, F$
$T \to F$
$F \to (\, E \,) $
$F \to id$

The parsing table is:

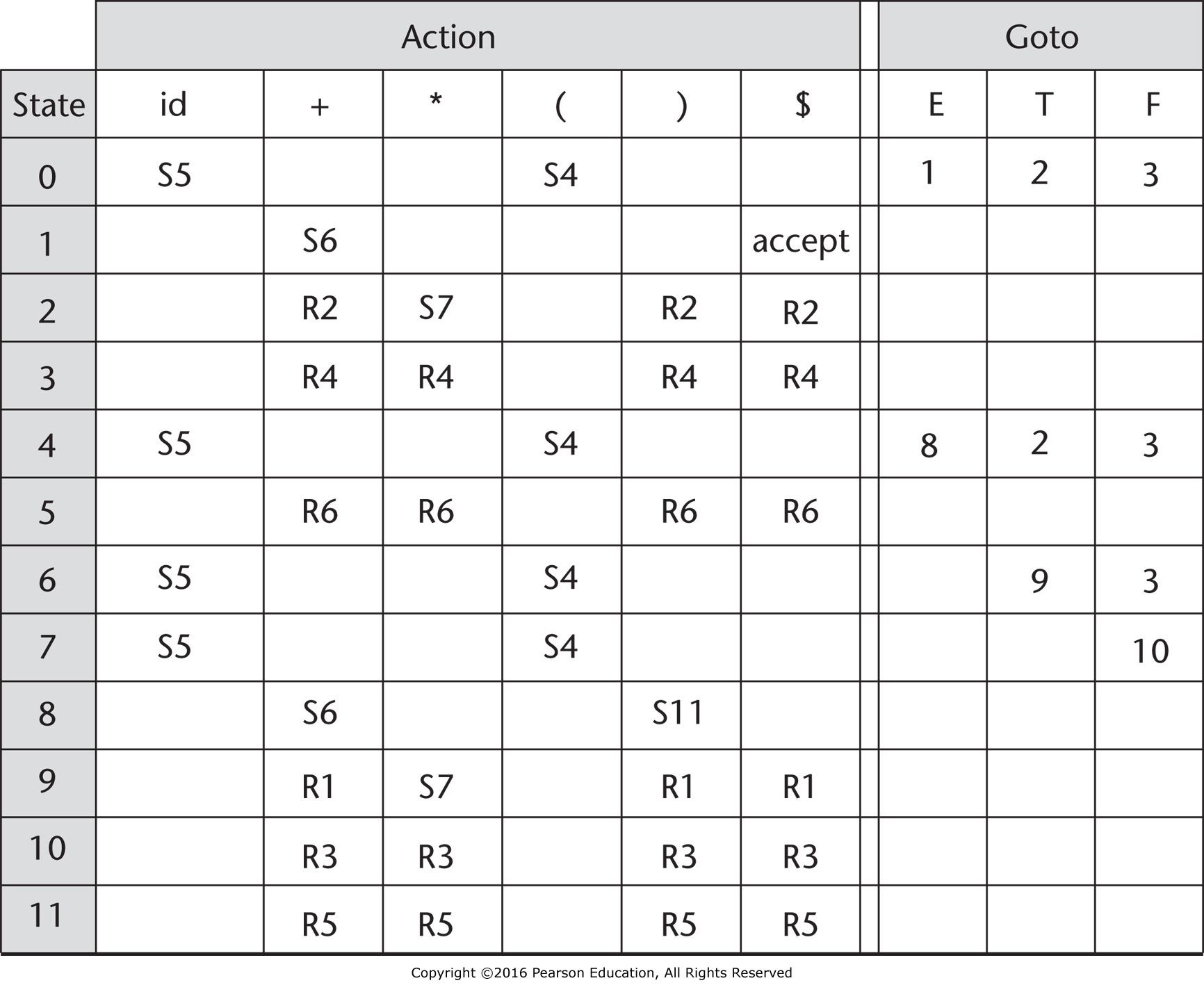
Stack	Input	Action
0	id + id\$	S5
0 id 5	+ id \$	R6
0 F 3	+ id \$	R4
0 T 2	+ id \$	R2
0 E 1	+ id \$	S6
0 E 1 + 6	id \$	S5
0 E 1 + 6 id 5	\$	R6
0 E 1 + 6 F 3	\$	R4
0 E 1 + 6 T 9	\$	R1
0 E 1	\$	accept

Bottom-Up Parsing¶

Show the parse including the stack for id * id

Grammar:

$E \to E \, + \, T$
$E \to T$
$T \to T \, * \, F$
$T \to F$
$F \to (\, E \,) $
$F \to id$

The parsing table is:

Stack	Input	Action
0	id * id\$	S5
0 id 5	* id \$	R6
0 F 3	* id \$	R4
0 T 2	* id \$	S7
0 T 2 * 7	id \$	S5
0 T 2 * 7 id 5	\$	R6
0 T 2 * 7 F 10	\$	R3
0 T 2	\$	R2
0 E 1	\$	accept

Procedural Languages (Lua)¶

Some advantages of Lua
How to read a basic Lua program
How to write simple Lua code

Lua Examples¶

What is the output of the following code? Given a short description in English as to what is being stored in the tables

funcs={}
for i=1,10 do
    table.insert(funcs, function() return i*i end)
end
funcs[2]()
funcs[3]()

4

9

Lua Examples¶

What is the output of this code and why?

function wrapper(a)
    local function square(a)
        return a^2
    end

    function cube(a)
        return a^3
    end

    return square(a)
end

print(wrapper(2))
print(cube(2))
print(square(2))

4
8
ERROR

Object-Oriented Languages (Java)¶

The principles of Object Oriented Programming
- What they mean
- How they are applied in Java
How to read Java
How to write simple Java code

Java Examples¶

What feature is the following code showing, and what is it meant as a compromise to?

public interface Camera{
   //functions here with no definition...
   //ex:
   //public void takePicture();
}
public interface MobilePhone{
   //functions here with no definition...
   //ex:
   //public void makeCall();
}
public class CameraPhone implements Camera, MobilePhone{
   //functions here...
}

This is showing using interfaces, which is a compromise to multiple inheritence

Java Examples¶

What technique is being shown below and what is the output of main?

class Point {
   protected int x, y;
   public Point() { this(0); }
   public Point(int x0) { this(x0, 0); }
   public Point(int x0, int y0) { x = x0; y = y0; }
   public Point(Point p) { this(p.x, p.y); }
   public int getX() { return x; }
   public int getY() { return y; }
   public int setX(int x0) { x = x0; }
   public int setY(int y0) { y = y0; }
   public void print() { System.out.println("Point"); }
}

public class Circle extends Point {
   private int r;
   public Circle(Point p) { this(p, 0); }
   public Circle(Point p, int r0) { super(p); r = r0; }
   public Circle() { this(0); }
   public Circle(int x0) { this(x0, 0); }
   public Circle(int x0, int y0) { this(x0, y0, 0); }
   public Circle(int x0, int y0, int r0) { super(x0, y0); r = r0; }
   public Circle(Circle c) { this(c.x, c.y, c.r); }
   public int getR() { return r; }
   public int setR(int r0) { r = r0; }
   public void print() { System.out.println("Circle"); }

   public static void main(String args[]) {
      Point p = new Point();
      Point c = new Circle();
      p.print();
      c.print();     
   }
}

Polymorphism is being shown, the output is
Point
Circle

Java Examples¶

Write a function that takes in an ArrayList or a LinkedList of any numeric type and returns the mean.

Java Examples¶

If time permits, finish Java example from previous lecture

Resources¶

Many of today's examples came from Rosetta Code