Parsing¶

Parsing Basics¶

Parsing or syntax anaylsis has two goals
- To find and report all syntax errors in the code
- To generate the syntactic structure of the code
We can parse any unambigous grammar in O($n^3$)
- By placing more restrictions on the form of the grammar, this can be reduced to O($n$)
There are two general parsing strategies
- Top Down, Start with the root and go to the leaves
- Bottom Up, Start with the leaves, work towards the root

Top-Down Parsing¶

Corresponds to a left-most derivation
Every Node is visited before visiting its branches
Two common implementations are recursive-descent parsing and table-driven parsing
- Both of these are LL algorithms, using a left-to-right scan on the input and a leftmost derivation

Resursive-Descent Parsing¶

Most popular Top-Down Parsing method
Is a collection of subprograms (functions)
- Each non-terminal in a grammar has exactly one subprogram associated with it
- We assume a global next_token that holds next token in the input
- We also assume that each subprogram leaves the global next_token on the token after it.

Recursive-Descent Parsing Example¶

For the grammar

$< term > \to < factor > \{(*|/)< factor >\}*$

We could use the following recursive descent parsing subprogram (this one is written in C)

void term() {
     factor(); /* parse first factor*/
     while (next_token == ast_code ||
            next_token == slash_code) {
         lexical(); /* get next token */
         factor(); /* parse next factor */
     }
 }

Recursive-Descent Problems¶

Cannot handle Grammars of the form
- $< expr > \to < expr > + < term >$
- Will always call the function expr, whose first call is to expr
Will have to do lots of backtracking for non-terminals that have many potential rules
- $< expr > \to < var > | < var > + < var > | < var > - < var > | < var > * < var> $
We can fix both these issues by rewritting the grammar

Removing Left Recursion¶

For a grammar of

$ S \to S \; \alpha $
$ S \to \beta $
$ \alpha $ , $ \beta$ are a mixture of terminals and non-terminals

We can remove left recursion by replacing S with

$ S \to \beta \; S' $
$ S' \to \alpha \; S' \, | \, \epsilon $

Removing Left Recursion Practice¶

Remove left recursion from

$ E \to E \, + \, T \, | \, T$
- $ E \to T \,E'$
- $ E' \to + \, T \, E' \, | \epsilon$
$ T \to T \, * \, F \, | \, F$
- $ T \to F \, T'$
- $ T' \to * \, F \, T' \, | \epsilon $

Left Factoring¶

The other issue for Recursive-Descent parsers are statements such as
- V $\to$ I | I [ E ]
- In both cases, the next token would be I, so our parser would have to guess
This can be rewritten as
- V $\to$ I N
- N $\to \epsilon$ | [ E ]

Bottom-Up Parsing¶

Starting with a string, we build the parse tree on top of it
- Does right most derivation in reverse
Can handle left recursion
At each step we need to find the handle
- The handle is portion of the mix of terminals and non-terminals that can simplified to another non-terminal
- A handle must lead to a valid derivation
- For the string id + id * id, id is the handle because we can simplfy to F + id * id

Shift-Reduce¶

The general algorithm used for bottom-up parsing
Uses the LR parsing strategy
- Scans strings from left-to-right
- Uses the rightmost derivation
Implemented using a parsing table and a stack
Shift pushes a token on to the stack while reduce uses a rule of the grammar to simplify part of the stack

Parse Tables¶

For the grammar:

$E \to E \, + \, T$
$E \to T$
$T \to T \, * \, F$
$T \to F$
$F \to (\, E \,) T$
$F \to id$

The parsing table is:

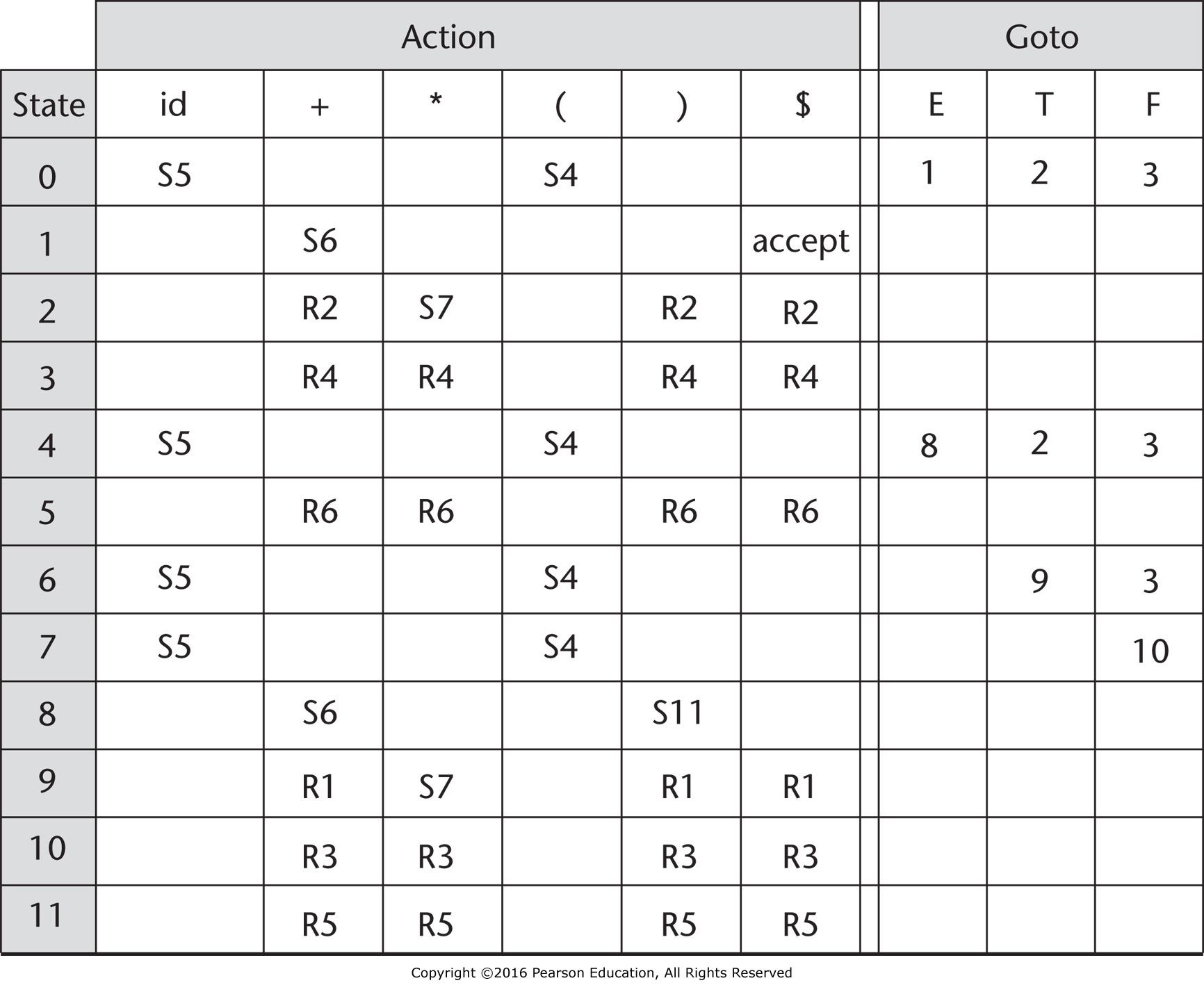
Shift-Reduce Algorithm¶

Initialize the stack with state 0
While not accept or error
- Given state and next symbol, find appropriate action in table
- If action is shift, we shift that symbol and new state onto the stack
- If action is reduce:
  - Pop handle and apply rule as indicated in table
  - Using next state on stack, look at goto table for new symbol and that state
  - Push non-terminal and state from goto on to stack

Shift-Reduce Algorithm Practice¶

Parse

Stack	Input	Action
0	id * id + id $	S5
0 id 5	* id + id $	R6
0 F 3	* id + id $	R4
0 T 2	* id + id $	S7
0 T 2 * 7	id + id $	S5
0 T 2 * 7 id 5	+ id $	R6
0 T 2 * 7 F 10	+ id $	R3
0 T 2	+ id $	R2
0 E 1	+ id $	S6
0 E 1 + 6	id $	S5
0 E 1 + 6 id 5	$	R6
0 E 1 + 6 F 3	$	R4
0 E 1 + 6 T 9	$	R1
0 E 1	$	accept

The parsing table is:

Shift-Reduce Practice¶

Show the parse including the stack for id * ( id + id)

Grammar:

$E \to E \, + \, T$
$E \to T$
$T \to T \, * \, F$
$T \to F$
$F \to (\, E \,) $
$F \to id$

The parsing table is:

Parse:

Stack	Input	Action
0	id * (id + id) $	S5
0 id 5	* (id + id) $	R6
0 F 3	* (id + id) $	R4
0 T 2	* (id + id) $	S7
0 T 2 * 7	(id + id) $	S4
0 T 2 * 7 ( 4	id + id ) $	S5
0 T 2 * 7 ( 4 id 5	+ id) $	R6
0 T 2 * 7 ( 4 F 3	+ id) $	R4
0 T 2 * 7 ( 4 T 2	+ id )$	R2
0 T 2 * 7 ( 4 E 8	+ id ) $	S6
0 T 2 * 7 ( 4 E 8 + 6	id )$	S5
0 T 2 * 7 ( 4 E 8 + 6 id 5	) $	R6
0 T 2 * 7 ( 4 E 8 + 6 F 3	) $	R4
0 T 2 * 7 ( 4 E 8 + 6 T 9	) $	R1
0 T 2 * 7 ( 4 E 8	) $	S11
0 T 2 * 7 ( 4 E 8 ) 11	$	R5
0 T 2 * 7 F 10	$	R3
0 T 2	$	R2
0 E 1	$	accept