Lexical Analysis

The Job of Lexical Analysis

• Read in characters from a file
• Determine the groupings of characters (the lexemes)
• Assign the lexemes to a token

Where Lexical Analysis Fits in

Methods of Lexical Anaylsis

Lexical Anaylsis boils down to matching patterns.
There are several ways to do this

• Use formal descriptions and regular expressions to describe the patterns
• Use a state transition diagram and accompying implementation
• Use a state transition diagram and manually construct a table-driven implentation

Regular Expressions

• A notation that is used to describe patterns
• Is simpler and less expresive than BNF
• Consists of three basic operations:
  • Concatenation ( ab )
  • Union a | b
  • Kleene Star or Kleene Closure a* = $\epsilon$|a|aa|aaa|....

Regular Expression Notataion

• Has some syntactic sugar that could be constructed from the above
  • Parentheses ( a ( b | c ) ) == ab|ac
  • Kleene Plus a+ == aa*
  • Zero or One Operator a? = a | $\epsilon$
  • Character classes [a-z] == a | b | c | ... | y | z

• Can use identifiers to break up long patterns
  • ONES = (one|two|three| ... | ten)
  • TEENS = (eleven|twelve|thirteen|...|nineteen)
  • TENS = (twenty|thirty|forty|...|ninety)
  • MONEY = ((ONES|TEENS)| TENS ONES)(CENTS | (DOLLARS ((ONES|TEENS)| TENS ONES) CENTS)
• Can be simplified even further
  • X = (ONES | TEENS)
  • Y = TENS ONES
  • NUMBER = (X | Y)
  • MONEY2 = NUMBER (CENTS | DOLLARS NUMBER CENTS)

RegEx Examples

Over the alphabet {a,b} give a regular expression for

• Strings with an even number of a's
  • (b*ab*ab*)* | b*
• Strings with a length that is a multiple of 3
  • ((a | b) (a | b) (a | b))*

Finite Automata

• A class of mathematical machines
• Represented by a state transition diagram
• Recognizes strings that can be described by regular expressions

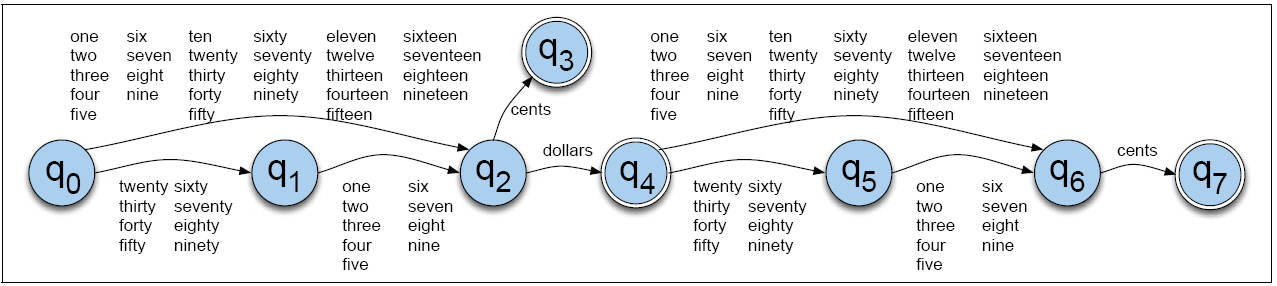
Deterministic Finite Automata

Finite automata that obey certain rules

• For each state, any given input only provides on possible trasition
• You cannot transition between two states with out looking at the input

DFA Practice

Over the alphabet {a,b} give a DFA that accepts:

• Strings with no more than 3 a's
• Strings with a length that is a multiple of 3

Lex

• Lexical analyzer generator
  • It writes a lexical analyzer
• Assumption
  • each token matches a regular expression
• Needs
  • set of regular expressions
  • for each expression an action
• Produces
  • A C program
• Automatically handles many tricky problems
• flex is the gnu version of the venerable unix tool lex.
  • Produces highly optimized code

Lex Example

/* scanner for a toy Pascal-like language */
%{
#include <math.h> /* needed for call to atof() */
%}
DIG [0-9]
ID [a-z][a-z0-9]*
%%
{DIG}+ printf("Integer: %s (%d)\n", yytext, atoi(yytext));
{DIG}+"."{DIG}* printf("Float: %s (%g)\n", yytext, atof(yytext));
if|then|begin|end printf("Keyword: %s\n",yytext);
{ID} printf("Identifier: %s\n",yytext);
"+"|"-"|"*"|"/" printf("Operator: %s\n",yytext);
"{"[^}\n]*"}" /* skip one-line comments */
[ \t\n]+ /* skip whitespace */
. printf("Unrecognized: %s\n",yytext);
%%
main(){yylex();}