Syntax

Definition

Adopted from Syntactic Theory 1999. Ivan A Sag & Thomas Wasow. pg 3

Syntax is the study of the ways in which variables, functions, expressions, and other parts of programming languages combine into statements, and statements into programs- the form or structure of well formed statements in a language.

From Syntactic Structure. 1957. Noam Chomsky

• Colorless green ideas sleep furiously
• Furiously sleep ideas green colorless

Mathmateical Description of a Language

An Alphabet ,$\Sigma$, is a set of characters
A Sentence is a a string from $\Sigma$
A Language ,L, is the set of all valid sentences.

Lexeme is the smallest syntactic unit. Approximates to a word in a natural language.
A Token is a category of lexemes. Approximates to a part of speech in a natural language.

Recognizers

One way to define a language L.

If we can build a machine, R, that has as input a string from $\Sigma$ and outputs if that string in is L, than R is a recognizer and is a complete description of L.

Compiliers use recognizers to anaylze a program and return if its valid for the language or contains errors. We will cover these a little bit more in a few weeks.

Generators

A hypothetical machine that returns a sentence for a given language L.

We actually care more about the structure of a generator than the output it can generate.

Backus-Naur Form (BNF)

• Primary method of syntax description in Computer Science
• Equivalent to Context Free grammars
• Is a metalanguage

BNF Basics

The definition of the syntax of a particular part of a languge is called a rule or production.

Takes the form

• LHS $\to$ RHS

LHS contains one nonterminal which represents a class of syntactic structures.
RHS contains both nonterminals and terminals - the lexemes and tokens of a language.

A grammar is a collection of rules.

BNF Example

$ < if\_stmt > \to$ if $ ( < logic\_expr >) < stmt > $
$ < if\_stmt > \to$ if $ ( < logic\_expr >) < stmt > $ else $< stmt >$

$< if\_stmt > \to$ if $ ( < logic\_expr >) < stmt > $ | if $ ( < logic\_expr >) < stmt > $ else $< stmt >$

Recursion

Some sytactic elements have an unknown number of pieces.
For example the following are all valid mathmateical expressions.

• 4 + 2
• 4 + 2 / 5
• 4 + 2 / 5 * 4

We can use a rule where the LHS is part of the RHS to create recursive rules

$< expr > \to < id > + < expr > | < id > * < expr >$
$ \qquad \qquad | \,(< expr >) | < id > $

BNF Practice

• Write a BNF rule for the first line of an address
  • 1000 Hilltop Circle
  • 1600 Pennsylvania Ave
  • 10 Downing Street

$< addr > \to < num > < street\_name > < street\_type >$
$< num > \to < digit >< num > | < digit> $
$< digit > \to 0 | 1 | 2 | 3 ... $

BNF Practice

• Write a BNF rule for the indexing into a list in python. As a reminder they can look like this

  • scores[0]
    

  • scores[3:]
    

  • scores[:2]
    

  • scores[1:4]
    

    $< array\_indx > \to < array\_name > [ < num > : < num > ] $
    $< array\_indx > \to < array\_name > [ : ] $
    $< array\_indx > \to < array\_name > [ < num > ] $
    $< array\_indx > \to < array\_name > [ : < num > ] $
    $< array\_name > \to < string > $
    $< string > \to < char > < string > | < char > $
    $< char > \to a | A | b | B | $

Derivation

A sequence of rule applications from the start symbol to a string in the language.

At each step in the sequence, replace a non-terminal with its RHS

We will use this grammar in the following example:

$< assign > \to < id > = < expr > $
$< id > \to A | B | C$
$< expr > \to < id > + < expr > $
$ \qquad \qquad | < id > * < expr > $
$ \qquad \qquad | \,(\, < expr > \,)\, $
$ \qquad \qquad | < id > $

Derivation (Cont'd)

Derivation for the string A = B * ( A + C)

$< assign > \Rightarrow < id > = < expr > $
$ \qquad \qquad \Rightarrow A = < expr > $
$ \qquad \qquad \Rightarrow A = < id > * < expr > $
$ \qquad \qquad \Rightarrow A = B * < expr > $
$ \qquad \qquad \Rightarrow A = B * ( < expr > ) $
$ \qquad \qquad \Rightarrow A = B * ( < id > + < expr > ) $
$ \qquad \qquad \Rightarrow A = B * ( A + < expr > ) $
$ \qquad \qquad \Rightarrow A = B * ( A + < id > ) $
$ \qquad \qquad \Rightarrow A = B * ( A + C) $

Derivation Practice

Given the following grammar:
S $\to$ a X
X $\to$ S b
X $\to$ b

Give a derivation for:

• ab
• aabb

$ S \Rightarrow a X$
$ \quad \Rightarrow a b$

$ S \Rightarrow a X$
$ \quad \Rightarrow a S b$
$ \quad \Rightarrow a a X b$
$ \quad \Rightarrow a a b b $

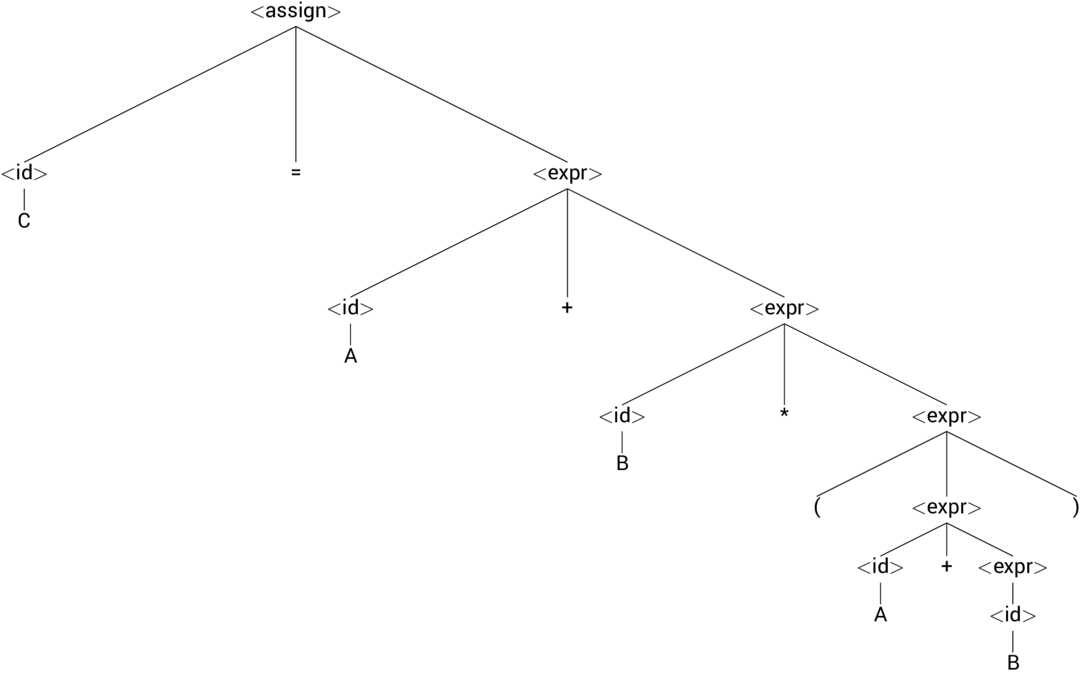
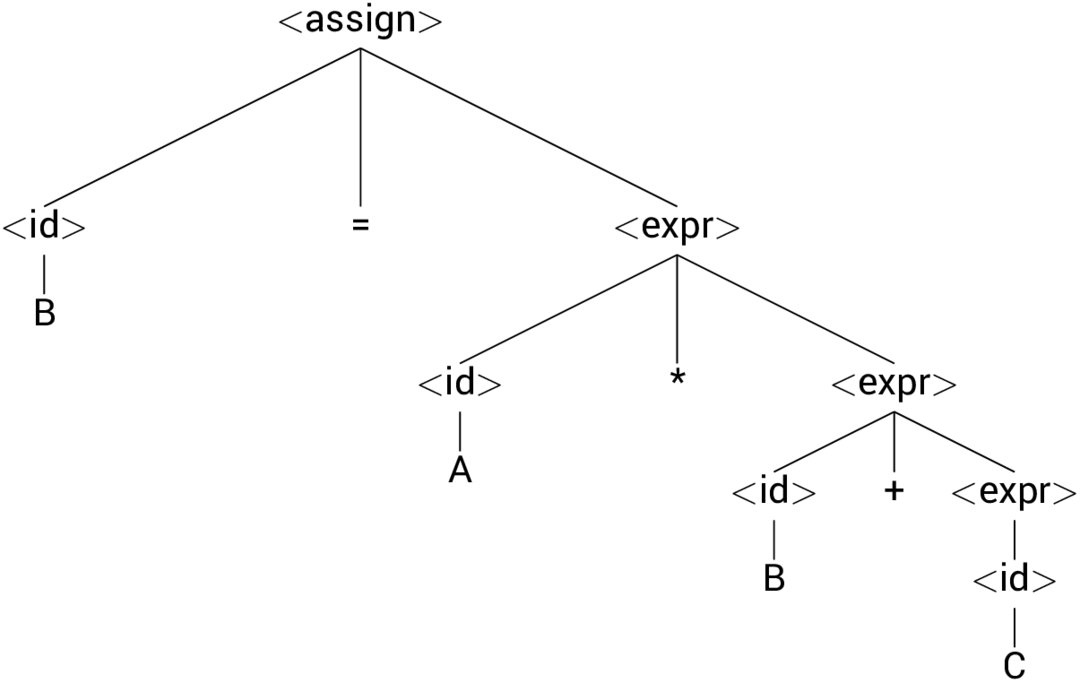
Parse Tree

Graphical representation of the heirarchy generated by a derivation

$< assign > \Rightarrow < id > = < expr > $ $ \qquad \qquad \Rightarrow A = < expr > $ $ \qquad \qquad \Rightarrow A = < id > * < expr > $ $ \qquad \qquad \Rightarrow A = B * < expr > $ $ \qquad \qquad \Rightarrow A = B * ( < expr > ) $ $ \qquad \qquad \Rightarrow A = B * ( < id > + < expr > ) $ $ \qquad \qquad \Rightarrow A = B * ( A + < expr > ) $ $ \qquad \qquad \Rightarrow A = B * ( A + < id > ) $ $ \qquad \qquad \Rightarrow A = B * ( A + C) $

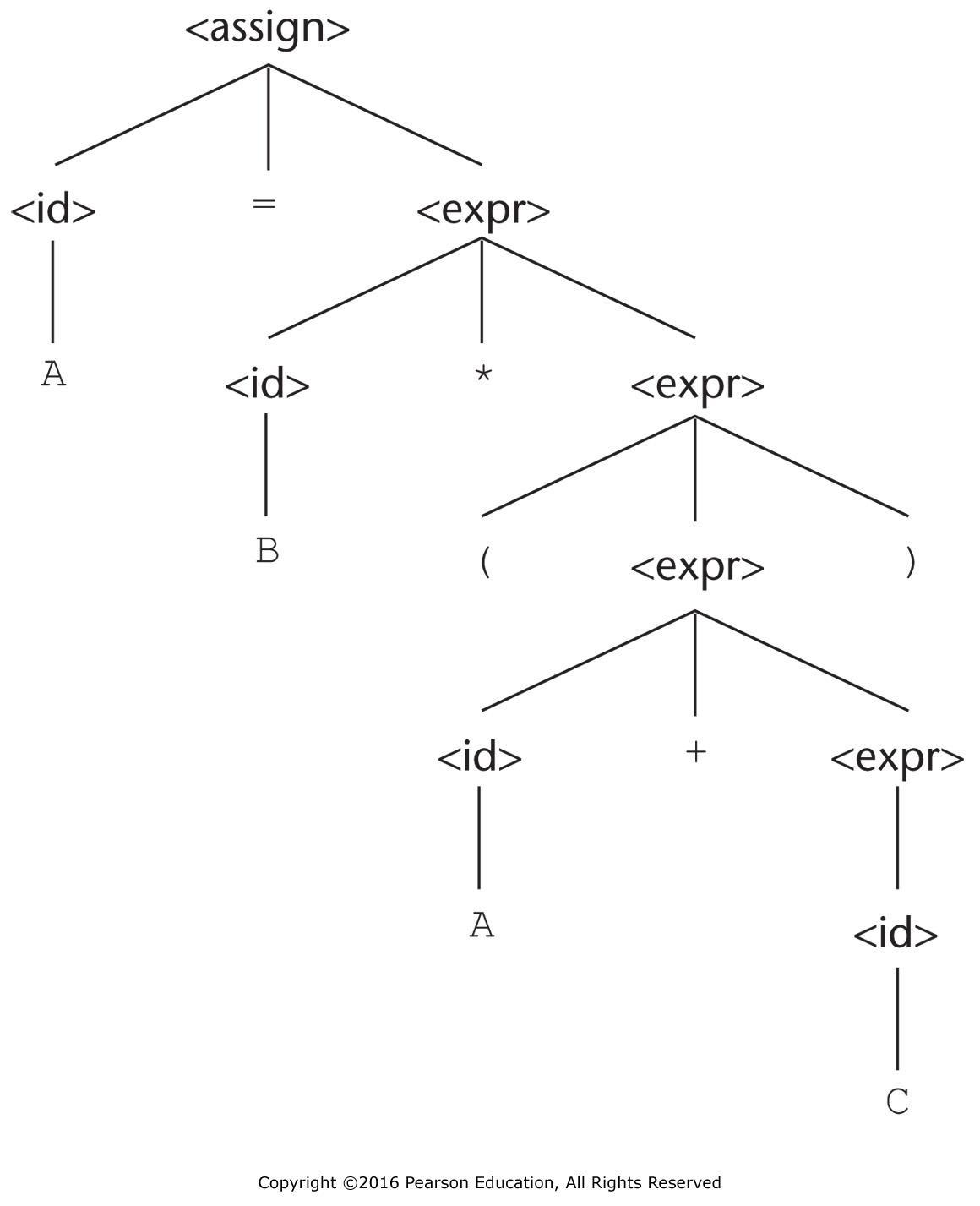
Parse Tree Practice

$< assign > \to < id > = < expr > $ $< id > \to A | B | C$ $< expr > \to < id > + < expr > $ $ \qquad \qquad | < id > * < expr > $ $ \qquad \qquad | \,(\, < expr > \,)\, $ $ \qquad \qquad | < id > $

Using the grammar on the left, draw the parse trees for:

• C = A + B \* (A + B)
• B = A \* B + C

Parse Tree Pracice Answers